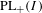Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-17T16:09:33.344Z Has data issue: false hasContentIssue false
  • English
  • Français

$\text{PL}_{+}(I)$ is not a Polish group

Published online by Cambridge University Press:  06 October 2015

MICHAEL P. COHEN  and
ROBERT R. KALLMAN
MICHAEL P. COHEN
Affiliation:
Department of Mathematics, North Dakota State University, PO Box 6050, Fargo, ND 58108-6050, USA email [email protected]
ROBERT R. KALLMAN
Affiliation:
Department of Mathematics, University of North Texas, 1155 Union Circle 311430, Denton, TX 76203-5017, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The group 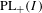$\text{PL}_{+}(I)$ of increasing piecewise-linear self-homeomorphisms of the interval 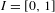$I=[0,1]$ may not be assigned a topology in such a way that it becomes a Polish group. The same statement holds for the groups 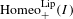$\text{Homeo}_{+}^{\text{Lip}}(I)$ of bi-Lipschitz homeomorphisms of $I$, and 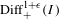$\text{Diff}_{+}^{1+\unicode[STIX]{x1D716}}(I)$ of diffeomorphisms of $I$ whose derivatives are Hölder continuous with exponent $\unicode[STIX]{x1D716}$, as well as the corresponding groups acting on the real line and on the circle.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 7 , October 2016 , pp. 2121 - 2137
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhmedov, A.. Questions and remarks on discrete and dense subgroups of Diff(I). J. Topol. Anal. 6(4) (2014), 557–571.Google Scholar
Arens, R. F.. A topology for spaces of transformations. Ann. of Math. (2) 47 (1946), 480–495.CrossRefGoogle Scholar
Becker, H. and Kechris, A. S.. The Descriptive Set Theory of Polish Group Actions (London Mathematical Society Lecture Note Series, 232) . Cambridge University Press, New York, 1996.Google Scholar
Bleak, C.. A geometric classification of some solvable groups of homeomorphisms. J. Lond. Math. Soc. 78 (2008), 352–372.Google Scholar
Brin, M. and Squier, C.. Presentations, conjugacy, roots, and centralizers in groups of piecewise linear homeomorphisms of the real line. Comm. Algebra 29 (2001), 4557–4596.Google Scholar
Dudley, R. M.. Continuity of homomorphisms. Duke Math. J. 28 (1961), 587–594.Google Scholar
Gao, S.. Invariant Descriptive Set Theory (Pure and Applied Mathematics) . Chapman & Hall/CRC Press, Boca Raton, FL, 2009.Google Scholar
Hayes, D.. Minimality of the special linear groups. PhD Thesis, University of North Texas, 1997.Google Scholar
Hjorth, G.. Classification and Orbit Equivalence Relations (Mathematical Surveys and Monographs, 75) . American Mathematical Society, Providence, RI, 2000.Google Scholar
Ibarlucía, T. and Melleray, J.. Full groups of minimal homeomorphisms and Baire category methods. Ergod. Th. & Dynam. Sys. 1–26; available on CJO2014, doi:10.1017/etds.2014.75.Google Scholar
Kallman, R. R.. Uniqueness results for homeomorphism groups. Trans. Amer. Math. Soc. 295 (1986), 389–396.CrossRefGoogle Scholar
Kechris, A. S.. Classical Descriptive Set Theory. Springer, New York, 1995.Google Scholar
Navas, A.. Groups of Circle Diffeomorphisms. University of Chicago Press, Chicago, IL, 2011.Google Scholar
Pestov, V.. Dynamics of Infinite-Dimensional Groups: The Ramsey–Dvoretzki–Milman Phenomenon. American Mathematical Society, Providence, RI, 2006.Google Scholar
Pettis, B. J.. On continuity and openness of homomorphisms in topological groups. Ann. of Math. (2) 52 (1950), 293–308.Google Scholar
Rosendal, C.. On the non-existence of certain group topologies. Fund. Math. 187(3) (2005), 213–228.CrossRefGoogle Scholar
Rubin, M.. On the reconstruction of topological spaces from their groups of homeomorphisms. Trans. Amer. Math. Soc. 312(2) (1989), 487–538.Google Scholar
Solecki, S.. Polish group topologies. Sets and Proofs (London Mathematical Society Lecture Note Series, 258) . Cambridge University Press, Cambridge, 1999, pp. 339–364.Google Scholar