Article contents
Templates for geodesic flows
Published online by Cambridge University Press: 28 November 2012
Abstract
We construct templates for geodesic flows on an infinite family of Hecke triangle groups. Our results generalize those of E. Ghys [Knots and dynamics. Proc. Int. Congress of Mathematicians. Vol. 1. International Congress of Mathematicians, Zürich, 2007], who constructed a template for the modular flow in the complement of the trefoil knot in 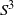 $S^3$. A significant difficulty that arises in any attempt to go beyond the modular flow is the fact that for other Hecke triangles the geodesic flow cannot be viewed as a flow in
$S^3$. A significant difficulty that arises in any attempt to go beyond the modular flow is the fact that for other Hecke triangles the geodesic flow cannot be viewed as a flow in 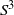 $S^3$, and one is led to consider embeddings into lens spaces. Our final result is an explicit description of a single ‘Hecke template’ which contains all other templates we construct, allowing a topological study of the periodic orbits of different Hecke triangle groups all at once.
$S^3$, and one is led to consider embeddings into lens spaces. Our final result is an explicit description of a single ‘Hecke template’ which contains all other templates we construct, allowing a topological study of the periodic orbits of different Hecke triangle groups all at once.
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Cambridge University Press
References
- 5
- Cited by


