Article contents
A symbolic characterization of the horseshoe locus in the Hénon family
Published online by Cambridge University Press: 08 March 2016
Abstract
We consider the family of quadratic Hénon diffeomorphisms of the plane 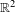 $\mathbb{R}^{2}$. A map will be said to be a ‘horseshoe’ if its restriction to the non-wandering set is hyperbolic and conjugate to the full 2-shift. We give a criterion for being a horseshoe based on an auxiliary coding which describes positions of points relative to the stable manifold of one of the fixed points. In addition we describe the topological conjugacy type of maps on the boundary of the horseshoe locus. We use complex techniques and we work with maps in a parameter region which is a two-dimensional analog of the familiar ‘
$\mathbb{R}^{2}$. A map will be said to be a ‘horseshoe’ if its restriction to the non-wandering set is hyperbolic and conjugate to the full 2-shift. We give a criterion for being a horseshoe based on an auxiliary coding which describes positions of points relative to the stable manifold of one of the fixed points. In addition we describe the topological conjugacy type of maps on the boundary of the horseshoe locus. We use complex techniques and we work with maps in a parameter region which is a two-dimensional analog of the familiar ‘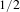 $1/2$-wake’ for the quadratic family
$1/2$-wake’ for the quadratic family 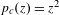 $p_{c}(z)=z^{2}$.
$p_{c}(z)=z^{2}$.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 6
- Cited by


