Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T02:17:26.994Z Has data issue: false hasContentIssue false
  • English
  • Français

Squirals and beyond: substitution tilings with singular continuous spectrum

Published online by Cambridge University Press:  20 March 2013

MICHAEL BAAKE  and
UWE GRIMM
MICHAEL BAAKE
Affiliation:
Fakultät für Mathematik, Universität Bielefeld, Postfach 100131, 33501 Bielefeld, Germany email [email protected]
UWE GRIMM
Affiliation:
Department of Mathematics and Statistics, The Open University, Walton Hall, Milton Keynes MK7 6AA, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

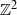The squiral inflation rule is equivalent to a bijective block substitution rule and leads to an interesting lattice dynamical system under the action of ${ \mathbb{Z} }^{2} $. In particular, its balanced version has purely singular continuous diffraction. The dynamical spectrum is of mixed type, with pure point and singular continuous components. We present a constructive proof that admits a generalization to bijective block substitutions of trivial height on 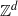${ \mathbb{Z} }^{d} $.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 4 , August 2014 , pp. 1077 - 1102
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alimov, Sh. A., Ashurov, R. R. and Pulatov, A. K.. Multiple Fourier series and Fourier integrals. Commutative Harmonic Analysis IV. Eds. Khavin, V. P. and Nikol’skiĭ, N. K.. Springer, Berlin, 1992, pp. 1–96.Google Scholar
Allouche, J.-P. and Shallit, J.. Automatic Sequences: Theory, Applications, Generalizations. Cambridge University Press, Cambridge, 2003.Google Scholar
Baake, M.. A guide to mathematical quasicrystals. Quasicrystals – An Introduction to Structure, Physical Properties and Applications. Eds. Suck, J.-B., Schreiber, M. and Häussler, P.. Springer, Berlin, 2002, pp. 17–48.Google Scholar
Baake, M.. Diffraction of weighted lattice subsets. Canad. Math. Bull. 45 (2002), 483–498.Google Scholar
Baake, M., Birkner, M. and Moody, R. V.. Diffraction of stochastic point sets: explicitly computable examples. Commun. Math. Phys. 293 (2010), 611–660.CrossRefGoogle Scholar
Baake, M., Gähler, F. and Grimm, U.. Spectral and topological properties of a family of generalised Thue–Morse sequences. J. Math. Phys. 53 (2012), 032701.Google Scholar
Baake, M., Gähler, F. and Grimm, U.. ‘Examples of substitution systems and their factors’, J. Integer Seq., to appear, arXiv:1211.5466.Google Scholar
Baake, M. and Grimm, U.. The singular continuous diffraction measure of the Thue–Morse chain. J. Phys. A: Math. Theor. 41 (2008), 422001.CrossRefGoogle Scholar
Baake, M. and Grimm, U.. Surprises in aperiodic diffraction. J. Phys.: Conf. Ser. 226 (2010), 012023.Google Scholar
Baake, M. and Grimm, U.. Kinematic diffraction from a mathematical viewpoint. Z. Krist. 226 (2011), 711–725.Google Scholar
Baake, M. and Grimm, U.. On the notions of symmetry and aperiodicity for Delone sets. Symmetry 4 (2012), 566–580.Google Scholar
Baake, M. and Lenz, D.. Dynamical systems on translation bounded measures: pure point dynamical and diffraction spectra. Ergod. Th. & Dynam. Sys. 24 (2004), 1867–1893.Google Scholar
Baake, M., Lenz, D. and Moody, R. V.. Characterization of model sets by dynamical systems. Ergod. Th. & Dynam. Sys. 27 (2007), 341–382.Google Scholar
Baake, M. and Moody, R. V.. Weighted Dirac combs with pure point diffraction. J. Reine Angew. Math. (Crelle) 573 (2004), 61–94.Google Scholar
Baake, M., Schlottmann, M. and Jarvis, P. D.. Quasiperiodic patterns with tenfold symmetry and equivalence with respect to local derivability. J. Phys. A: Math. Gen. 24 (1991), 4637–4654.Google Scholar
Baake, M. and Ward, T.. Planar dynamical systems with pure Lebesgue diffraction spectrum. J. Stat. Phys. 140 (2010), 90–102.Google Scholar
Bauer, H.. Measure and Integration Theory. de Gruyter, Berlin, 2001.Google Scholar
Billingsley, P.. Probability and Measure, 3rd edn. Wiley, New York, 1995.Google Scholar
Cheng, Z., Savit, R. and Merlin, R.. Structure and electronic properties of Thue–Morse lattices. Phys. Rev. B 37 (1988), 4375–4382.Google Scholar
Cortez, M. I., Durand, F. and Petite, S.. Linearly repetitive Delone systems have a finite number of non-periodic Delone system factors. Proc. Amer. Math. Soc. 138 (2010), 1033–1046.Google Scholar
Cowley, J. M.. Diffraction Physics, 3rd edn. North-Holland, Amsterdam, 1995.Google Scholar
Dekking, F. M.. The spectrum of dynamical systems arising from substitutions of constant length. Z. Wahrscheinlichkeitsth. verw. Geb. 41 (1978), 221–239.Google Scholar
Frank, N. P.. Multi-dimensional constant-length substitution sequences. Topol. Appl. 152 (2005), 44–69.Google Scholar
Frank, N. P.. Spectral theory of bijective substitution sequences. MFO Reports 6 (2009), 752–756.Google Scholar
Frettlöh, D.. Nichtperiodische Pflasterungen mit ganzzahligem Inflationsfaktor. PhD Thesis, University of Dortmund, 2002.Google Scholar
Frettlöh, D. and Sing, B.. Computing modular coincidences for substitution tilings and point sets. Discrete Comput. Geom. 37 (2007), 381–407.CrossRefGoogle Scholar
Gähler, F. and Klitzing, R.. The diffraction pattern of self-similar tilings. The Mathematics of Long-Range Aperiodic Order (NATO ASI C 489). Ed. Moody, R. V.. Kluwer, Dordrecht, 1997, pp. 141–174.Google Scholar
Gnedenko, B. V.. The Theory of Probability and The Elements of Statistics, 4th edn. AMS Chelsea, Providence, RI, 2005, reprint.Google Scholar
Godrèche, C. and Luck, J. M.. Multifractal analysis in reciprocal space and the nature of the Fourier transform of self-similar structures. J. Phys. A: Math. Gen. 23 (1990), 3769–3797.CrossRefGoogle Scholar
Grünbaum, B. and Shephard, G. C.. Tilings and Patterns. Freeman, New York, 1987.Google Scholar
Höffe, M. and Baake, M.. Surprises in diffuse scattering. Z. Krist. 215 (2000), 441–444.Google Scholar
Hof, A.. On diffraction by aperiodic structures. Commun. Math. Phys. 169 (1995), 25–43.Google Scholar
Kakutani, S.. Strictly ergodic symbolic dynamical systems. Proc. 6th Berkeley Symposium on Math. Statistics and Probability. Eds. LeCam, L. M., Neyman, J. and Scott, E. L.. University of California Press, Berkeley, CA, 1972, pp. 319–326.Google Scholar
Katznelson, Y.. An Introduction to Harmonic Analysis, 3rd edn. Cambridge University Press, New York, 2004.Google Scholar
Keane, M.. Generalized Morse sequences. Z. Wahrscheinlichkeitsth. verw. Geb. 10 (1968), 335–353.Google Scholar
Knill, O.. Singular continuous spectrum and quantitative rates of weak mixing. Discrete Contin. Dyn. Syst. 4 (1998), 33–42.Google Scholar
Lagarias, J. C. and Pleasants, P. A. B.. Repetitive Delone sets and quasicrystals. Ergod. Th. & Dynam. Sys. 23 (2003), 831–867.Google Scholar
Lee, J.-Y. and Moody, R. V.. Lattice substitution systems and model sets. Discrete Comput. Geom. 25 (2001), 173–201.Google Scholar
Lee, J.-Y., Moody, R. V. and Solomyak, B.. Pure point dynamical and diffraction spectra. Ann. Henri Poincaré 3, (2002), 1003–1018.Google Scholar
Lee, J.-Y., Moody, R. V. and Solomyak, B.. Consequences of pure point diffraction spectra for multiset substitution systems. Discrete Comput. Geom. 29 (2003), 525–560.Google Scholar
Lenz, D. and Moody, R. V.. Stationary processes with pure point diffraction. Preprint, arXiv:1111.3617.Google Scholar
Mahler, K.. The spectrum of an array and its application to the study of the translation properties of a simple class of arithmetical functions. Part II: On the translation properties of a simple class of arithmetical functions. J. Math. Massachusetts 6 (1927), 158–163.Google Scholar
Nadkarni, M. G.. Basic Ergodic Theory, 2nd edn. Birkhäuser, Basel, 1995.Google Scholar
Pedersen, G. K.. Analysis Now. Springer, New York, 1995, revised printing.Google Scholar
Pinsky, M. A.. Introduction to Fourier Analysis and Wavelets. Brooks/Cole, Pacific Grove, CA, 2002.Google Scholar
Queffélec, M.. Spectral study of automatic and substitutive sequences. Beyond Quasicrystals. Eds. Axel, F. and Gratias, D.. Springer, Berlin, 1995, pp. 369–414.Google Scholar
Queffélec, M.. Substitution Dynamical Systems – Spectral Analysis, (Lecture Notes in Mathe matics, 1294), 2nd edn. Springer, Berlin, 2010.CrossRefGoogle Scholar
Robinson, E. A.. On the table and the chair. Indag. Math. (N.S.) 10 (1999), 581–599.Google Scholar
Robinson, E. A.. Symbolic dynamics and tilings of ${ \mathbb{R} }^{d} $. Proc. Sympos. Appl. Math. 60 (2004), 81–119.Google Scholar
Rudin, W.. Fourier Analysis on Groups. Wiley, New York, 1990, reprint.Google Scholar
Schlottmann, M.. Generalised model sets and dynamical systems. Directions in Mathematical Quasicrystals (CRM Monograph Series, 13). Eds. Baake, M. and Moody, R. V.. American Mathematical Society, Providence, RI, 2000, pp. 143–159.Google Scholar
Solomyak, B.. Dynamics of self-similar tilings. Ergod. Th. & Dynam. Sys. 17 (1997), 695–738; Erratum Ergod. Th. & Dynam. Sys. 19 (1999) 1685.Google Scholar
Solomyak, B.. Private communication, 2012.Google Scholar
Tucker, H. G.. A Graduate Course in Probability. Academic Press, New York, 1967.Google Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer, New York, 2000, reprint.Google Scholar
Wiener, N.. The spectrum of an array and its application to the study of the translation properties of a simple class of arithmetical functions. Part I: The spectrum of an array. J. Math. Massachusetts 6 (1927), 145–157.Google Scholar
Withers, R. L.. Disorder, structured diffuse scattering and the transmission electron microscope. Z. Krist. 220 (2005), 1027–1034.Google Scholar
Zaks, M. A.. On the dimensions of the spectral measure of symmetric binary substitutions. J. Phys. A: Math. Gen. 35 (2002), 5833–5841.Google Scholar
Zygmund, A.. Trigonometric Series, 3rd edn. Cambridge University Press, Cambridge, 2002.Google Scholar