Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lifshits, Mikhail
and
Weber, Michel
1998.
High Dimensional Probability.
p.
249.
Jones, Roger L.
Rosenblatt, Joseph M.
and
Wierdl, Máté
1999.
Counting in Ergodic Theory.
Canadian Journal of Mathematics,
Vol. 51,
Issue. 5,
p.
996.
Jones, Roger L.
and
Rosenblatt, Joseph M.
2000.
Reverse inequalities.
The Journal of Fourier Analysis and Applications,
Vol. 6,
Issue. 3,
p.
325.
Gaposhkin, V. F.
2000.
On the Integrability of a Maximal Square Function in Ergodic Theory.
Theory of Probability & Its Applications,
Vol. 44,
Issue. 2,
p.
386.
Campbell, James T.
Jones, Roger L.
Reinhold, Karin
and
Wierdl, Máté
2000.
Oscillation and variation for the Hilbert transform.
Duke Mathematical Journal,
Vol. 105,
Issue. 1,
Campbell, James
Jones, Roger
Reinhold, Karin
and
Wierdl, Máté
2002.
Oscillation and variation for singular integrals in higher dimensions.
Transactions of the American Mathematical Society,
Vol. 355,
Issue. 5,
p.
2115.
Lifshits, Mikhail
and
Weber, Michel
2003.
Régularisation spectrale et propriétés métriques des moyennes mobiles.
Journal d'Analyse Mathématique,
Vol. 89,
Issue. 1,
p.
1.
LIU, CHAOYUAN
2010.
Strong bounded operators for ergodic averages and Lebesgue derivatives.
Ergodic Theory and Dynamical Systems,
Vol. 30,
Issue. 2,
p.
547.
Aliev, Ilham A.
and
Bayrakci, Simten
2011.
Square-like Functions Generated by a Composite Wavelet Transform.
Mediterranean Journal of Mathematics,
Vol. 8,
Issue. 4,
p.
553.
Viola, P. S.
and
Viviani, B. E.
2012.
An explicit expression for singular integral operators with non-necessarily doubling measures.
Collectanea Mathematica,
Vol. 63,
Issue. 2,
p.
217.
Kohlenbach, U.
and
Leuştean, L.
2012.
Effective metastability of Halpern iterates in CAT(0) spaces.
Advances in Mathematics,
Vol. 231,
Issue. 5,
p.
2526.
Kohlenbach, Ulrich
and
Safarik, Pavol
2014.
Fluctuations, effective learnability and metastability in analysis.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 1,
p.
266.
Keleş, Şeyda
and
Bayrakçı, Simten
2014.
Square-like functions generated by the Laplace-Bessel differential operator.
Advances in Difference Equations,
Vol. 2014,
Issue. 1,
Bui, The Anh
2014.
Boundedness of variation operators and oscillation operators for certain semigroups.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 106,
Issue. ,
p.
124.
AVIGAD, JEREMY
and
RUTE, JASON
2015.
Oscillation and the mean ergodic theorem for uniformly convex Banach spaces.
Ergodic Theory and Dynamical Systems,
Vol. 35,
Issue. 4,
p.
1009.
KOVAČ, VJEKOSLAV
2016.
Quantitative norm convergence of double ergodic averages associated with two commuting group actions.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 3,
p.
860.
Zhang, Jing
and
Wu, Huo Xiong
2017.
Weighted oscillation and variation inequalities for singular integrals and commutators satisfying Hörmander type conditions.
Acta Mathematica Sinica, English Series,
Vol. 33,
Issue. 10,
p.
1397.
Bayrakci, Simten
2018.
On the boundedness of square function generated by the Bessel differential operator in weighted LebesqueLp,αspaces.
Open Mathematics,
Vol. 16,
Issue. 1,
p.
730.
DURCIK, POLONA
KOVAČ, VJEKOSLAV
ŠKREB, KRISTINA ANA
and
THIELE, CHRISTOPH
2019.
Norm variation of ergodic averages with respect to two commuting transformations.
Ergodic Theory and Dynamical Systems,
Vol. 39,
Issue. 3,
p.
658.
Kovač, Vjekoslav
and
Stipčić, Mario
2020.
Convergence of ergodic–martingale paraproducts.
Statistics & Probability Letters,
Vol. 164,
Issue. ,
p.
108826.


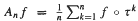 in ergodic theory, let
in ergodic theory, let 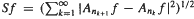 . There is a strong inequality ‖
. There is a strong inequality ‖