Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:39:19.614Z Has data issue: false hasContentIssue false
  • English
  • Français

The spectrum of Poincaré recurrence

Published online by Cambridge University Press:  15 September 2008

KA-SING LAU  and
LIN SHU
KA-SING LAU
Affiliation:
Department of Mathematics, The Chinese University of Hong Kong, Shatin, Hong Kong (email: [email protected])
LIN SHU
Affiliation:
Department of Mathematics, The Chinese University of Hong Kong, Shatin, Hong Kong (email: [email protected]) School of Mathematical Sciences, Peking University, Beijing 100871, People’s Republic of China (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

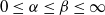We investigate the relationship between Poincaré recurrence and topological entropy of a dynamical system (X,f). For , let D(α,β) be the set of x with lower and upper recurrence rates α and β, respectively. Under the assumptions that the system is not minimal and that the map f is positively expansive and satisfies the specification condition, we show that for any open subset 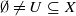, 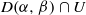has the full topological entropy of X. This extends a result of Feng and Wu [The Hausdorff dimension of recurrence sets in symbolic spaces. Nonlinearity14 (2001), 81–85] for symbolic spaces.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 6 , December 2008 , pp. 1917 - 1943
Copyright
Copyright © 2008 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Barreira, L. M.. A non-additive thermodynamic formalism and applications to dimension theory of hyperbolic dynamical systems. Ergod. Th. & Dynam. Sys. 16 (1996), 871–927.Google Scholar
[2] Barreira, L. and Saussol, B.. Hausdorff dimension of measures via Poincaré recurrence. Comm. Math. Phys. 219 (2001), 443–463.Google Scholar
[3] Barreira, L. and Saussol, B.. Product structure of Poincaré recurrence. Ergod. Th. & Dynam. Sys. 22 (2002), 33–61.CrossRefGoogle Scholar
[4] Blanchard, F.. β-Expansions and symbolic dynamics. Theoret. Comput. Sci. 65 (1989), 131–141.CrossRefGoogle Scholar
[5] Bowen, R.. Periodic points and measures for Axiom A diffeomorphism. Trans. Amer. Math. Soc. 154 (1971), 377–397.Google Scholar
[6] Bowen, R.. Topological entropy for non-compact sets. Trans. Amer. Math. Soc. 49 (1973), 125–136.Google Scholar
[7] Brin, M. and Katok, A.. On Local Entropy. Geometric dynamics (Rio de Janeiro) (1981) (Lecture Notes in Mathematics, 1007). Springer, Berlin, 1983, pp. 30–38.Google Scholar
[8] Cutler, C. D.. Connecting ergodicity and dimension in dynamical systems. Ergod. Th. & Dynam. Sys. 10 (1990), 451–462.Google Scholar
[9] Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527). Springer, Berlin, 1976.CrossRefGoogle Scholar
[10] Downarowicz, T. and Weiss, B.. Entropy theorems along times when x visits a set. Illinois. J. Math. 48 (2004), 59–69.CrossRefGoogle Scholar
[11] Edgar, G. A. and Mauldin, R. D.. Multifractal decompositions of digraph recursive fractals. Proc. London Math. Soc. 65 (1992), 604–628.Google Scholar
[12] Eisenberg, M.. Expansive transformation semigroups of automorphisms. Fund. Math. 59 (1966), 313–321.CrossRefGoogle Scholar
[13] Fan, A.-H. and Feng, D.-J.. On the distribution of long-term time averages on symbolic space. J. Stat. Phys. 99(3–4) (2000), 813–856.CrossRefGoogle Scholar
[14] Fan, A.-H., Feng, D.-J. and Wu, J.. Recurrence, dimension and entropy. J. London Math. Soc. 64 (2001), 229–244.CrossRefGoogle Scholar
[15] Feng, D.-J. and Wu, J.. The Hausdorff dimension of recurrence sets in symbolic spaces. Nonlinearity 14 (2001), 81–85.Google Scholar
[16] Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. de l’IHÉS. 51 (1980), 137–173.CrossRefGoogle Scholar
[17] Mauldin, R. D. and Williams, S. C.. Hausdorff dimension in graph directed constructions. Trans. Amer. Math. Soc. 309 (1988), 811–829.Google Scholar
[18] Moran, P. A. P.. Additive functions of intervals and Hausdorff measure. Proc. Cambridge Philos. Soc. 42 (1946), 15–23.Google Scholar
[19] Olsen, L.. First return times: multifractal spectra and divergence points. Discrete Contin. Dyn. Syst. Ser. A 10 (2004), 635–656.CrossRefGoogle Scholar
[20] Ornstein, D. S. and Weiss, B.. Entropy and data compression schemes. IEEE Trans. Inform. Theory 39 (1993), 78–83.Google Scholar
[21] Pesin, Y. B.. Dimension Theory in Dynamical Systems. University of Chicago Press, Chicago, 1997.CrossRefGoogle Scholar
[22] Pesin, Y. B. and Weiss, H.. On the dimension of deterministic and random Cantor-like sets, symbolic dynamics, and the Eckmann-Ruelle conjecture. Comm. Math. Phys. 182 (1996), 105–153.Google Scholar
[23] Reddy, W. L.. Expanding maps on compact metric spaces. Topology Appl. 13 (1982), 327–334.CrossRefGoogle Scholar
[24] Rosenholtz, I.. Local expansions, derivatives, and fixed points. Fund. Math. 91 (1976), 1–4.Google Scholar
[25] Ruelle, D.. Thermodynamic Formalism. The Mathematical Structures of Classical Equilibrium Statistical Mechanics (Encyclopedia of Mathematics and its Applications, 5). Addison-Wesley, Reading, MA, 1978.Google Scholar
[26] Saussol, B., Troubetzkoy, S. and Vaienti, S.. Recurrence, dimensions and Lyapunov exponents. J. Stat. Phys. 106 (2002), 623–634.CrossRefGoogle Scholar
[27] Saussol, B. and Wu, J.. Recurrence spectrum in smooth dynamical system. Nonlinearity 16 (2003), 1991–2001.Google Scholar
[28] Schmeling, J.. Symbolic dynamics for β-shifts and self-normal numbers. Ergod. Th. & Dynam. Sys. 17 (1997), 675–694.CrossRefGoogle Scholar
[29] Shu, L.. Poincaré recurrence, measure theoretic and topological entropy. PhD Thesis, CUHK, 2007.Google Scholar
[30] Sigmund, K.. On dynamical systems with the specification property. Trans. Amer. Math. Soc. 190 (1974), 285–289.Google Scholar
[31] Takens, F. and Verbitskiy, E.. On the variational principle for the topological entropy of certain non-compact sets. Ergod. Th. & Dynam. Sys. 23 (2003), 317–348.CrossRefGoogle Scholar
[32] Walters, P.. An Introduction to Ergodic theory (Graduate Texts in Mathematics, 79). Springer, Berlin, 1982.Google Scholar
[33] Williams, R. F.. A note on unstable homeomorphism. Proc. Amer. Math. Soc. 6 (1955), 308–309.CrossRefGoogle Scholar