Published online by Cambridge University Press: 19 September 2008
Let f be a piecewise monotone map of the interval [0,1] to itself, and g a function of bounded variation on [0, 1]. Hofbauer, Keller and Rychlik have studied operators 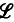 on functions of bounded variation, where
on functions of bounded variation, where
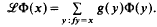
Among other things, they show that the essential spectral radius of 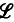 is in many cases strictly smaller than the spectral radius; there exist therefore isolated eigenvalues of finite multiplicity. The purpose of the present paper is to prove similar results for a more general class of operators forming an algebra (and therefore containing sums of operators like
is in many cases strictly smaller than the spectral radius; there exist therefore isolated eigenvalues of finite multiplicity. The purpose of the present paper is to prove similar results for a more general class of operators forming an algebra (and therefore containing sums of operators like 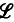 ). An analogous extension was presented by Ruelle for operators associated with expanding maps.
). An analogous extension was presented by Ruelle for operators associated with expanding maps.