No CrossRef data available.
Published online by Cambridge University Press: 16 December 2011
We extend the idea of bilateral determinism of a free Z-action by D. Ornstein and B. Weiss to a free Z2-action. We show that we have a ‘stronger’ spatial determinism for Z2-actions: to determine the complete Z2-name of a point, it is enough to know the name of a fraction of the orbit whose density can be made arbitrarily small. Moreover, for zero-entropy Z2-actions, we prove that there exists a partition 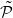 such that the
such that the 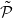 -names of an arbitrarily small one-sided cone determine the points.
-names of an arbitrarily small one-sided cone determine the points.