Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:36:43.111Z Has data issue: false hasContentIssue false
  • English
  • Français

Sofic entropy of Gaussian actions

Published online by Cambridge University Press:  12 May 2016

BEN HAYES
BEN HAYES*
Affiliation:
Stevenson Center, Nashville, TN 37240, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Associated to any orthogonal representation of a countable discrete group, is a probability measure-preserving action called the Gaussian action. Using the Polish model formalism we developed before, we compute the entropy (in the sense of Bowen [J. Amer. Math. Soc.23 (2010) 217–245], Kerr and Li [Invent. Math.186 (2011) 501–558]) of Gaussian actions when the group is sofic. Computation of entropy for Gaussian actions has only been done when the acting group is abelian and thus our results are new, even in the amenable case. Fundamental to our approach are methods of non-commutative harmonic analysis and 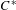$C^{\ast }$-algebras which replace the Fourier analysis used in the abelian case.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 7 , October 2017 , pp. 2187 - 2222
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bowen, L.. Measure conjugacy invariants for actions of countable sofic groups. J. Amer. Math. Soc. 23 (2010), 217–245.Google Scholar
Bowen, L.. Entropy for expansive algebraic actions of residually finite groups. Ergod. Th. & Dynam. Sys. 31(3) (2011), 703–718.Google Scholar
Bowen, L.. Weak isomorphisms between Bernoulli shifts. Israel J. Math. 183 (2011).Google Scholar
Bowen, L.. Every countably infinite group is almost Ornstein. Dynamical Systems and Group Actions. Vol. 567 (Contemporary Mathematics) . American Mathematical Society, Providence, RI, 2012, pp. 67–78.Google Scholar
Bowen, L. and Li, H.. Harmonic models and spanning forests of residually finite groups. J. Funct. Anal. 263(7) (2012), 1769–1808.Google Scholar
Brown, N. and Ozawa, N.. C ∗ -Algebras and Finite-Dimensional Approximations. American Mathematical Society, Providence, RI, 1994.Google Scholar
Ciobanu, L., Holt, D. and Rees, S.. Sofic groups: graph products and graphs of groups. Pacific J. Math. 271(1) (2014), 53–64.Google Scholar
Conway, J.. A Course in Operator Theory (Graduate Studies in Mathematics) . American Mathematical Society, Providence, RI, 1991.Google Scholar
Dooley, A. and Golodets, V.. The spectrum of completely positive entropy actions of countable amenable groups. J. Funct. Anal. 196(1) (2002), 1–18.Google Scholar
Dykema, K., Kerr, D. and Pichot, M.. Orbit equivalence and sofic approximation. Preprint, 2011,arXiv:1102.2556.Google Scholar
Dykema, K., Kerr, D. and Pichot, M.. Sofic dimension for discrete measurable groupoids. Trans. Amer. Math. Soc. 366(2) (2013), 707–748.Google Scholar
Elek, G. and Szabo, E.. On sofic groups. J. Group Theory 9(2) (2006), 161–171.Google Scholar
Folland, G.. Real Analysis: Modern Techinques and Their Applications, 2nd edn. Wiley, Hoboken, NJ, 1999.Google Scholar
Friedman, J.. A proof of Alon’s second eigenvalue conjecture and related problems. Mem. Amer. Math. Soc. 195 (2008), 1–100.Google Scholar
Hayes, B.. Fuglede-Kadison determinants and sofic entropy. Preprint, 2014, arXiv:1402.1135.Google Scholar
Hayes, B.. An l p -version of von Neumann dimension for Banach space representations of sofic groups. J. Funct. Anal. 266(2) (2014), 989–1040.Google Scholar
Hayes, B.. Polish models and sofic entropy. J. Inst. Math. Jussieu to appear.Google Scholar
Kerr, D.. Bernoulli actions of sofic groups have completely positive entropy. Israel J. Math. 202(1) (2014), 461–474.Google Scholar
Kerr, D. and Li, H.. Topological entropy and the variational principle for actions of sofic groups. Invent. Math. 186 (2011), 501–558.Google Scholar
Kieffer, J.. A generalized Shannon-McMillan theorem for the action of an amenable group on a probability space. Ann. Probab. 3(6) (1975), 1031–1037.CrossRefGoogle Scholar
Lemańczyk, M.. Entropy of Gaussian actions for countable abelian groups. Fund. Math. 157 (1998), 277–286.Google Scholar
Meyerovitch, T.. Positive sofic entropy implies finite stabilizer. Preprint, 2015, arXiv:1504.08137.CrossRefGoogle Scholar
Nica, A.. Asymptotically free families of random unitaries in symmetric groups. Pacific J. Math. 157 (1993), 295–310.CrossRefGoogle Scholar
Ornstein, D. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.Google Scholar
Paunescu, L.. On sofic actions and equivalence relations. J. Funct. Anal. 261(9) (2011), 2461–2485.CrossRefGoogle Scholar
Paunescu, L.. Convex structures revisited. Ergod. Th. & Dynam. Sys. to appear doi:10.1017/etds.2014.129.CrossRefGoogle Scholar
Peterson, J. and Sinclair, T.. On cocycle superrigidity for Gaussian actions. Ergod. Th. & Dynam. Sys. 32(1) (2012), 249–272.Google Scholar
Popa, S.. Independence properties in subagebras of ultraproduct II1 factors. J. Funct. Anal. 266(9) (2014), 5818–5846.CrossRefGoogle Scholar
Seward, B.. Every action of a non-amenable group is the factor of a small action. J. Mod. Dyn. 8(2) (2014), 251–270.CrossRefGoogle Scholar
Takesaki, M.. The Theory of Operator Algebras I. Springer, Berlin, 2002.Google Scholar
Takesaki, M.. Theory of Operator Algebras II (Encyclopaedia of Mathematical Sciences, 125) . Springer, New York, 2003.Google Scholar