Article contents
Simultaneous linearization of germs of commuting holomorphic diffeomorphisms
Published online by Cambridge University Press: 14 September 2011
Abstract
Let α1,…,αn be irrational numbers which are linearly independent over the rationals, and f1,…,fn commuting germs of holomorphic diffeomorphisms in ℂ such that fk(0)=0,f′k(0)=e2πiαk,k=1,…,n. Moser showed that f
1,…,fn are simultaneously linearizable (i.e. conjugate by a germ of holomorphic diffeomorphism h to the rigid rotations Rαk(z)=e2πiαkz) if the vector of rotation numbers (α
1,…,αn) satisfies a Diophantine condition. Adapting Yoccoz’s renormalization to the setting of commuting germs, we show that simultaneous linearization holds in the presence of a weaker Brjuno-type condition ℬ(α1,…,αn)<+∞, where ℬ(α1,…,αn) is a multivariable analogue of the Brjuno function. If there are no periodic orbits for the action of the germs f1,…,fn in a neighbourhood of the origin, then a weaker arithmetic condition ℬ′ (α
1,…,αn)<+∞ analogous to Perez-Marco’s condition for linearization in the absence of periodic orbits is shown to suffice for linearizability. Normalizing the germs to be univalent on the unit disc, in both cases the Siegel discs are shown to contain discs of radii 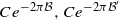 for some universal constant C.
for some universal constant C.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 2
- Cited by


