Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T00:21:57.035Z Has data issue: false hasContentIssue false
  • English
  • Français

Simultaneous dense and non-dense orbits for certain partially hyperbolic diffeomorphisms

Part of: Smooth dynamical systems: general theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  04 September 2018

WEISHENG WU
WEISHENG WU*
Affiliation:
Department of Applied Mathematics, College of Science, China Agricultural University, Beijing, 100083, PR China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 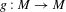$g:M\rightarrow M$ be a 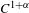$C^{1+\unicode[STIX]{x1D6FC}}$-partially hyperbolic diffeomorphism preserving an ergodic normalized volume on 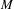$M$. We show that, if 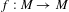$f:M\rightarrow M$ is a 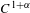$C^{1+\unicode[STIX]{x1D6FC}}$-Anosov diffeomorphism such that the stable subspaces of 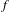$f$ and $g$ span the whole tangent space at some point on 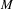$M$, the set of points that equidistribute under $g$ but have non-dense orbits under 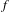$f$ has full Hausdorff dimension. The same result is also obtained when 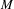$M$ is the torus and 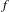$f$ is a toral endomorphism whose center-stable subspace does not contain the stable subspace of $g$ at some point.

Keywords

Nondense orbitsSchmidt gamespartial hyperbolicitydimension theory

MSC classification

Primary: 37D30: Partially hyperbolic systems and dominated splittings
Secondary: 37C45: Dimension theory of dynamical systems
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 4 , April 2020 , pp. 1083 - 1107
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anosov, D. V.. Geodesic flows on closed Riemann manifolds with negative curvature. Proc. Steklov Inst. Math. 90 (1967), 1–235.Google Scholar
Anosov, D. V. and Sinai, Y. G.. Some smooth ergodic systems. Russian Math. Surveys 22(5) (1967), 103–167.Google Scholar
Bergelson, V., Einsiedler, M. and Tseng, J.. Simultaneous dense and nondense orbits for commuting maps. Israel J. Math. 210(1) (2015), 23–45.Google Scholar
Brin, M. and Katok, A.. On local entropy. Geometric Dynamics (Rio de Janeiro, 1981) (Lecture Notes in Mathematics, 1007). Springer, Berlin, 1983, pp. 30–38.Google Scholar
Brin, M. and Pesin, Ya. B.. Partially hyperbolic dynamical systems. Izv. Acad. Nauk SSSR 38 (1974), 177–212.Google Scholar
Brin, M. and Stuck, G.. Introduction to Dynamical Systems. Cambridge University Press, Cambridge, 2002.Google Scholar
Broderick, R., Fishman, L. and Kleinbock, D. Y.. Schmidt’s game, fractals, and orbits of toral endomorphisms. Ergod. Th. & Dynam. Sys. 31 (2011), 1095–1107.Google Scholar
Dani, S. G.. On orbits of endomorphisms of tori and the Schmidt game. Ergod. Th. & Dynam. Sys. 8(4) (1988), 523–529.Google Scholar
Dolgopyat, D.. Bounded orbits of Anosov flows. Duke Math. J. 87(1) (1997), 87–114.Google Scholar
Einsiedler, M. and Maier, A.. Simultaneous equidistributing and non-dense points for non-commuting toral automorphisms. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2018.30. Published online 11 May 2018.Google Scholar
Franks, J. M.. Invariant sets of hyperbolic toral automorphisms. Amer. J. Math. 99(5) (1977), 1089–1095.Google Scholar
Gatzouras, D. and Peres, Y.. Invariant measures of full dimension for some expanding maps. Ergod. Th. & Dynam. Sys. 17(1) (1997), 147–167.Google Scholar
Hasselblatt, B.. Regularity of the Anosov splitting and of horospheric foliations. Ergod. Th. & Dynam. Sys. 14(4) (1994), 645–666.Google Scholar
Hochman, M.. Lectures on dynamics, fractal geometry, and metric number theory. J. Mod. Dyn. 8(3–4) (2014), 437–497.Google Scholar
Kleinbock, D. Y. and Margulis, G. A.. Bounded orbits of nonquasiunipotent flows on homogeneous spaces. Amer. Math. Soc. Transl. 171 (1996), 141–172.Google Scholar
Lytle, B. and Maier, A.. Simultaneous dense and nondense orbits for noncommuting toral endomorphisms. Monatsh. Math. 185(3) (2018), 473–488.Google Scholar
McMullen, C.. Area and Hausdorff dimension of Julia sets of entire functions. Trans. Amer. Math. Soc. 300(1) (1987), 329–342.Google Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A. and Ures, R.. A survey of partially hyperbolic dynamics. Partially Hyperbolic Dynamics, Laminations, and Teichmüller Flow (Fields Institute Communications, 51). American Mathematical Society, Providence, RI, 2007, pp. 35–87.Google Scholar
Rokhlin, V. A.. On the fundamental ideas of measure theory. Amer. Math. Soc. Transl. 71 (1952), 55 pp. Transl. from Mat. Sbornik 25 (1949), 107–150.Google Scholar
Schmidt, W. M.. On badly approximable numbers and certain games. Trans. Amer. Math. Soc. 123(1) (1966), 178–199.Google Scholar
Shi, R. and Tseng, J.. Simultaneous dense and nondense orbits and the space of lattices. Int. Math. Res. Not. IMRN 2015(21) (2015), 11276–11288.Google Scholar
Tseng, J.. Schmidt games and Markov partitions. Nonlinearity 22(3) (2009), 525–543.Google Scholar
Tseng, J.. Nondense orbits for Anosov diffeomorphisms of the 2-torus. Real Anal. Exchange 41(2) (2016), 307–314.Google Scholar
Tseng, J.. Simultaneous dense and non-dense orbits for toral diffeomorphisms. Ergod. Th. & Dynam. Sys. 37(4) (2017), 1308–1322.Google Scholar
Urbański, M.. The Hausdorff dimension of the set of points with nondense orbit under a hyperbolic dynamical system. Nonlinearity 4(2) (1991), 385–397.Google Scholar
Wu, W.. Schmidt games and non-dense forward orbits of certain partially hyperbolic systems. Ergod. Th. & Dynam. Sys. 36(5) (2016), 1656–1678.Google Scholar
Wu, W.. Modified Schmidt games and non-dense forward orbits of partially hyperbolic systems. Discrete Contin. Dyn. Syst. Ser. A 36(6) (2016), 3463–3481.Google Scholar
Wu, W.. On non-dense orbits of certain non-algebraic dynamical systems. J. Dynam. Differential Equations 30(2) (2018), 501–519.Google Scholar
Young, L. S.. Dimension, entropy and Lyapunov exponents. Ergod. Th. & Dynam. Sys. 2(01) (1982), 109–124.Google Scholar