Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T16:53:15.283Z Has data issue: false hasContentIssue false
  • English
  • Français

Rotation number and one-parameter families of circle diffeomorphisms

Published online by Cambridge University Press:  19 September 2008

Masato Tsujii
Masato Tsujii
Affiliation:
Department of Mathematics, Kyoto University, Sakyo-ku, Kyoto, 606, Japan
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider one-parameter families of circle diffeomorphisms, f1(x) = f(x) + t(t ∈ S1), where f: S1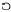 is a Cr-diffeomorphism (r≥3). We show that, for Lebesgue almost every t ∈ S1 the rotation number of f1, is either a rational number or an irrational number of Roth type. In the former case, f1, has periodic orbits and, in the latter case, f1, is Cr − 2-conjugate to an irrational rigid rotation from well-known theorems of Herman and Yoccoz.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 12 , Issue 2 , June 1992 , pp. 359 - 363
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[A]Arnol'd, V. I.. Small denominators I; On the mappings of a circle into itself. Trans. Amer. Math. Soc. 46 (1961), 213–284.Google Scholar
[H1]Herman, M. R.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. math. IHES 49 (1979), 5–234.CrossRefGoogle Scholar
[H2]Herman, M. R.. Mesure de Lebesgue et nombre de rotation. Lecture notes in mathematics 597 (Springer: New York, 1977), pp. 271–293.Google Scholar
[T]Tsujii, M.. A measure on the space of mappings and dynamical system theory. J. Math. Soc. Japan, to appear.Google Scholar
[Y]Yoccoz, J. C.. Conjugaison différentiable des difféomorphismes du cercle dont le nombre de rotation vérifie une condition Diophantienne. Ann. Sci. de I' Ec. Norm. Sup. 17 (1984), 333–361.CrossRefGoogle Scholar