Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T11:00:03.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Representations of Cuntz algebras associated to quasi-stationary Markov measures

Published online by Cambridge University Press:  30 June 2014

DORIN ERVIN DUTKAY  and
PALLE E. T. JORGENSEN
DORIN ERVIN DUTKAY
Affiliation:
University of Central Florida, Department of Mathematics, 4000 Central Florida Blvd., P.O. Box 161364, Orlando, FL 32816-1364, USA email [email protected]
PALLE E. T. JORGENSEN
Affiliation:
University of Iowa, Department of Mathematics, 14 MacLean Hall, Iowa City, IA 52242-1419, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

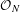In this paper, we answer the question of equivalence, or singularity, of two given quasi-stationary Markov measures on one-sided infinite words, as well as the corresponding question of equivalence of associated Cuntz algebra ${\mathcal{O}}_{N}$-representations. We do this by associating certain monic representations of 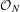${\mathcal{O}}_{N}$ to quasi-stationary Markov measures and then proving that equivalence for a pair of measures is decided by unitary equivalence of the corresponding pair of representations.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 7 , October 2015 , pp. 2080 - 2093
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, M. and Kawamura, K.. Branching laws for endomorphisms of fermions and the Cuntz algebra 𝓞2. J. Math. Phys. 49(4) (2008), 043501.CrossRefGoogle Scholar
Akin, H.. An upper bound of the directional entropy with respect to the Markov measures. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 22(11) (2012), 1250263.CrossRefGoogle Scholar
Bratteli, O. and Jorgensen, P. E. T.. Wavelet filters and infinite-dimensional unitary groups. Wavelet Analysis and Applications (Guangzhou, 1999) (AMS/IP Studies in Advanced Mathematics, 25). American Mathematical Society, Providence, RI, 2002, pp. 35–65.Google Scholar
Bratteli, O. and Robinson, D. W.. Operator Algebras and Quantum Statistical Mechanics 2: Equilibrium States. Models in Quantum Statistical Mechanics (Texts and Monographs in Physics). Springer, New York, 1981.CrossRefGoogle Scholar
Burgstaller, B.. Slightly larger than a graph C ∗ -algebra. Israel J. Math. 144 (2004), 1–14.CrossRefGoogle Scholar
Cuntz, J.. Simple C ∗ -algebras generated by isometries. Comm. Math. Phys. 57(2) (1977), 173–185.CrossRefGoogle Scholar
Cuntz, J.. Noncommutative Haar measure and algebraic finiteness conditions for simple C ∗ -algebras. Algèbres d’Opérateurs et Leurs Applications en Physique Mathématique (Marseille, 1977) (Colloques internationaux du Centre national de la recherche scientifique, 274). CNRS, Paris, 1979, pp. 113–133.Google Scholar
Dutkay, D. E., Han, D. and Jorgensen, P. E. T.. Orthogonal exponentials, translations, and Bohr completions. J. Funct. Anal. 257(9) (2009), 2999–3019.CrossRefGoogle Scholar
Dutkay, D. E., Haussermann, J. and Jorgensen, P. E. T.. Atomic representations of Cuntz algebras. Preprint, arXiv:1311.5265, 2013.Google Scholar
Dutkay, D. E. and Jorgensen, P. E. T.. Wavelets on fractals. Rev. Mat. Iberoam. 22(1) (2006), 131–180.CrossRefGoogle Scholar
Dutkay, D. E. and Jorgensen, P. E. T.. Analysis of orthogonality and of orbits in affine iterated function systems. Math. Z. 256(4) (2007), 801–823.CrossRefGoogle Scholar
Dutkay , D. E. and Jorgensen, P. E. T.. Martingales, endomorphisms, and covariant systems of operators in Hilbert space. J. Operator Theory 58(2) (2007), 269–310.Google Scholar
Dutkay, D. E. and Jorgensen, P. E. T.. Fourier series on fractals: a parallel with wavelet theory. Radon Transforms, Geometry, and Wavelets (Contemporary Mathematics, 464). American Mathematical Society, Providence, RI, 2008, pp. 75–101.CrossRefGoogle Scholar
Dutkay, D. E. and Jorgensen, P. E. T.. Affine fractals as boundaries and their harmonic analysis. Proc. Amer. Math. Soc. 139(9) (2011), 3291–3305.CrossRefGoogle Scholar
Dutkay, D. E. and Jorgensen, P. E. T.. Spectral measures and Cuntz algebras. Math. Comp. 81(280) (2012), 2275–2301.CrossRefGoogle Scholar
Dutkay, D. E. and Jorgensen, P. E. T.. Monic representations of the Cuntz algebra and Markov measures. Preprint, arXiv:1401.2186, 2014.CrossRefGoogle Scholar
Dutkay, D. E., Picioroaga, G. and Song, M.-S.. Orthonormal bases generated by Cuntz algebras. J. Math. Anal. Appl. 409(2) (2014), 1128–1139.CrossRefGoogle Scholar
Engelbert, H. J. and Shiryaev, A. N.. On absolute continuity and singularity of probability measures. Mathematical Statistics (Banach Center Publications, 6). PWN, Warsaw, 1980, pp. 121–132.Google Scholar
Glimm, J. G.. On a certain class of operator algebras. Trans. Amer. Math. Soc. 95 (1960), 318–340.CrossRefGoogle Scholar
Grigorchuk, R. and Nekrashevych, V.. Self-similar groups, operator algebras and Schur complement. J. Mod. Dyn. 1(3) (2007), 323–370.CrossRefGoogle Scholar
Giordano, T., Putnam, I. F. and Skau, C. F.. Topological orbit equivalence and C ∗ -crossed products. J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Hida, T.. Brownian Motion (Applications of Mathematics, 11). Springer, New York, 1980, translated from the Japanese by the author and T. P. Speed.CrossRefGoogle Scholar
Jorgensen, P. E. T.. Minimality of the data in wavelet filters. Adv. Math. 159(2) (2001), 143–228.CrossRefGoogle Scholar
Jorgensen, P. E. T.. Analysis and Probability: Wavelets, Signals, Fractals (Graduate Texts in Mathematics, 234). Springer, New York, 2006.Google Scholar
Jorgensen, P. E. T. and Paolucci, A. M.. Markov measures and extended zeta functions. J. Appl. Math. Comput. 38(1–2) (2012), 305–323.CrossRefGoogle Scholar
Kakutani, S.. On equivalence of infinite product measures. Ann. of Math. (2) 49 (1948), 214–224.CrossRefGoogle Scholar
Kawamura, K.. Generalized permutative representation of Cuntz algebra. I: generalization of cycle type. Sūrikaisekikenkyūsho Kōkyūroku 1300 (2003), 1–23. The structure of operator algebras and its applications (Japanese) (Kyoto, 2002).Google Scholar
Kawamura, K.. Branching laws for polynomial endomorphisms of Cuntz algebras arising from permutations. Lett. Math. Phys. 77(2) (2006), 111–126.CrossRefGoogle Scholar
Kawamura, K.. Universal fermionization of bosons on permutative representations of the Cuntz algebra 𝓞2. J. Math. Phys. 50(5) (2009), 053521.CrossRefGoogle Scholar
Kawamura, K., Hayashi, Y. and Lascu, Dan. Continued fraction expansions and permutative representations of the Cuntz algebra 𝓞∞. J. Number Theory 129(12) (2009), 3069–3080.CrossRefGoogle Scholar
Seneta, E.. Non-negative matrices and Markov chains (Springer Series in Statistics). Springer, New York, 2006, revised reprint of the second (1981) edition.Google Scholar
Shiryaev, A. N.. Probability (Graduate Texts in Mathematics, 95), 2nd edn. Springer, New York, 1996, translated from the first (1980) Russian edition by R. P. Boas.CrossRefGoogle Scholar
Skau, C.. Orbit structure of topological dynamical systems and its invariants. Operator Algebras and Quantum Field Theory (Rome, 1996). International Press, Cambridge, MA, 1997, pp. 533–544.Google Scholar
Strichartz, R. S.. Besicovitch meets Wiener–Fourier expansions and fractal measures. Bull. Amer. Math. Soc. (N.S.) 20(1) (1989), 55–59.CrossRefGoogle Scholar