Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T20:37:43.080Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative bifurcation sets and the local dimension of univoque bases

Part of: Elementary number theory Topological dynamics Classical measure theory

Published online by Cambridge University Press:  26 May 2020

PIETER ALLAART  and
DERONG KONG
PIETER ALLAART
Affiliation:
Mathematics Department, University of North Texas, 1155 Union Cir #311430, Denton, TX76203-5017, USA (e-mail: [email protected])
DERONG KONG
Affiliation:
College of Mathematics and Statistics, Chongqing University, 401331, Chongqing, PR China (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Fix an alphabet 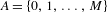$A=\{0,1,\ldots ,M\}$ with 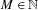$M\in \mathbb{N}$. The univoque set 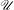$\mathscr{U}$ of bases 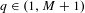$q\in (1,M+1)$ in which the number $1$ has a unique expansion over the alphabet $A$ has been well studied. It has Lebesgue measure zero but Hausdorff dimension one. This paper describes how the points in the set 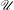$\mathscr{U}$ are distributed over the interval 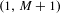$(1,M+1)$ by determining the limit

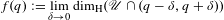$$\begin{eqnarray}f(q):=\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\dim _{\text{H}}(\mathscr{U}\cap (q-\unicode[STIX]{x1D6FF},q+\unicode[STIX]{x1D6FF}))\end{eqnarray}$$
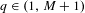for all $q\in (1,M+1)$. We show in particular that 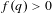$f(q)>0$ if and only if 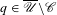$q\in \overline{\mathscr{U}}\backslash \mathscr{C}$, where 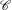$\mathscr{C}$ is an uncountable set of Hausdorff dimension zero, and 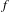$f$ is continuous at those (and only those) points where it vanishes. Furthermore, we introduce a countable family of pairwise disjoint subsets of 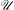$\mathscr{U}$ called relative bifurcation sets, and use them to give an explicit expression for the Hausdorff dimension of the intersection of 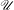$\mathscr{U}$ with any interval, answering a question of Kalle et al [On the bifurcation set of unique expansions. Acta Arith. 188 (2019), 367–399]. Finally, the methods developed in this paper are used to give a complete answer to a question of the first author [On univoque and strongly univoque sets. Adv. Math.308 (2017), 575–598] on strongly univoque sets.

Keywords

univoque basesHausdorff dimensionbifurcation setrelative entropy plateaustrongly univoque set

MSC classification

Primary: 11A63: Radix representation; digital problems
Secondary: 37B10: Symbolic dynamics 28A80: Fractals
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 8 , August 2021 , pp. 2241 - 2273
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barrera, R. A.. Topological and ergodic properties of symmetric sub-shifts. Discrete Contin. Dyn. Syst. 34(11) (2014), 4459–4486.Google Scholar
Barrera, R. A., Baker, S. and Kong, D.. Entropy, topological transitivity, and dimensional properties of unique q-expansions. Trans. Amer. Math. Soc. 371 (2019), 3209–3258.Google Scholar
Allaart, P. C.. The infinite derivatives of Okamoto’s self-affine functions: an application of 𝛽-expansions. J. Fractal Geom. 3(1) (2016), 1–31.Google Scholar
Allaart, P. C.. On univoque and strongly univoque sets. Adv. Math. 308 (2017), 575–598.Google Scholar
Allaart, P. C.. An algebraic approach to entropy plateaus in non-integer base expansions. Discrete Contin. Dyn. Syst. A 39(11) (2019), 6507–6522.Google Scholar
Allaart, P. C., Baker, S. and Kong, D.. Bifurcation sets arising from non-integer base expansions. J. Fractal Geom. 6(4) (2019), 301–341.Google Scholar
Allaart, P. C. and Kong, D.. On the continuity of the Hausdorff dimension of the univoque set. Adv. Math. 354 (2019), 106729.Google Scholar
Allouche, J.-P. and Cosnard, M.. Itérations de fonctions unimodales et suites engendrées par automates. C. R. Acad. Sci. Paris Sér. I Math. 296(3) (1983), 159–162.Google Scholar
Allouche, J.-P. and Cosnard, M.. Non-integer bases, iteration of continuous real maps, and an arithmetic self-similar set. Acta Math. Hungar. 91(4) (2001), 325–332.Google Scholar
Baiocchi, C. and Komornik, V.. Greedy and quasi-greedy expansions in non-integer bases. Preprint, 2007, arXiv:0710.3001v1.Google Scholar
Baker, S.. On small bases which admit countably many expansions. J. Number Theory 147 (2015), 515–532.Google Scholar
Baker, S. and Sidorov, N.. Expansions in non-integer bases: lower order revisited. Integers 14 (2014), Paper No. A57, 15.Google Scholar
Bonanno, C., Carminati, C., Isola, S. and Tiozzo, G.. Dynamics of continued fractions and kneading sequences of unimodal maps. Discrete Contin. Dyn. Syst. 33(4) (2013), 1313–1332.Google Scholar
Dajani, K. and de Vries, M.. Invariant densities for random 𝛽-expansions. J. Eur. Math. Soc. (JEMS) 9(1) (2007), 157–176.Google Scholar
Dajani, K., Komornik, V., Kong, D. and Li, W.. Algebraic sums and products of univoque bases. Indag. Math. 29 (2018), 1087–1104.Google Scholar
Daróczy, Z. and Kátai, I.. On the structure of univoque numbers. Publ. Math. Debrecen 46(3-4) (1995), 385–408.Google Scholar
de Vries, M. and Komornik, V.. Unique expansions of real numbers. Adv. Math. 221(2) (2009), 390–427.Google Scholar
de Vries, M., Komornik, V. and Loreti, P.. Topology of the set of univoque bases. Topology Appl. 205 (2016), 117–137.Google Scholar
Erdős, P., Joó, I. and Komornik, V.. Characterization of the unique expansions 1 =∑ i=1 ∞ q -n i and related problems. Bull. Soc. Math. France 118 (1990), 377–390.Google Scholar
Erdős, P., Horváth, M. and Joó, I.. On the uniqueness of the expansions 1 =∑ q -n i . Acta Math. Hungar. 58(3–4) (1991), 333–342.Google Scholar
Erdős, P. and Joó, I.. On the number of expansions 1 =∑ q -n i . Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 35 (1992), 129–132.Google Scholar
Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons Ltd., Chichester, 1990.Google Scholar
Glendinning, P. and Sidorov, N.. Unique representations of real numbers in non-integer bases. Math. Res. Lett. 8 (2001), 535–543.Google Scholar
Jordan, T., Shmerkin, P. and Solomyak, B.. Multifractal structure of Bernoulli convolutions. Math. Proc. Cambridge Phil. Soc. 151(3) (2011), 521–539.Google Scholar
Kalle, C., Kong, D., Li, W. and Lü, F.. On the bifurcation set of unique expansions. Acta Arith. 188 (2019), 367–399.Google Scholar
Komornik, V. and Kong, D.. Bases in which some numbers have exactly two expansions. J. Number Theory 195 (2019), 226–268.Google Scholar
Komornik, V., Kong, D. and Li, W.. Hausdorff dimension of univoque sets and devil’s staircase. Adv. Math. 305 (2017), 165–196.Google Scholar
Komornik, V. and Loreti, P.. Unique developments in non-integer bases. Amer. Math. Monthly 105(7) (1998), 636–639.Google Scholar
Komornik, V. and Loreti, P.. Subexpansions, superexpansions and uniqueness properties in non-integer bases. Period. Math. Hungar. 44(2) (2002), 197–218.Google Scholar
Komornik, V. and Loreti, P.. On the topological structure of univoque sets. J. Number Theory 122(1) (2007), 157–183.Google Scholar
Kong, D. and Li, W.. Hausdorff dimension of unique beta expansions. Nonlinearity 28(1) (2015), 187–209.Google Scholar
Kong, D., Li, W. and Dekking, F. M.. Intersections of homogeneous Cantor sets and beta-expansions. Nonlinearity 23(11) (2010), 2815–2834.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Lü, F. and Wu, J.. Diophantine analysis in beta-dynamical systems and Hausdorff dimensions. Adv. Math. 290 (2016), 919–937.Google Scholar
Parry, W.. On the 𝛽-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.Google Scholar
Rényi, A.. Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hungar. 8 (1957), 477–493.Google Scholar
Sidorov, N.. Almost every number has a continuum of 𝛽-expansions. Amer. Math. Monthly 110(9) (2003), 838–842.Google Scholar
Sidorov, N.. Combinatorics of linear iterated function systems with overlaps. Nonlinearity 20(5) (2007), 1299–1312.Google Scholar
Sidorov, N.. Expansions in non-integer bases: lower, middle and top orders. J. Number Theory 129(4) (2009), 741–754.Google Scholar