Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T16:55:17.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Recurrence, rigidity, and popular differences

Published online by Cambridge University Press:  28 September 2017

JOHN T. GRIESMER
JOHN T. GRIESMER*
Affiliation:
Department of Applied Mathematics & Statistics, Colorado School of Mines, 1500 Illinois Street, Golden, CO 80401, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a set of integers $S$ such that every translate of $S$ is a set of recurrence and a set of rigidity for a weak mixing measure preserving system. Here ‘set of rigidity’ means that enumerating $S$ as 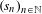$(s_{n})_{n\in \mathbb{N}}$ produces a rigidity sequence. This construction generalizes or strengthens results of Katznelson, Saeki (on equidistribution and the Bohr topology), Forrest (on sets of recurrence and strong recurrence), and Fayad and Kanigowski (on rigidity sequences). The construction also provides a density analogue of Julia Wolf’s results on popular differences in finite abelian groups.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 5 , May 2019 , pp. 1299 - 1316
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergelson, V.. Sets of recurrence of Z m -actions and properties of sets of differences in Z m . J. Lond. Math. Soc. (2) 31(2) (1985), 295–304.Google Scholar
Bergelson, V., del Junco, A., Lemańczyk, M. and Rosenblatt, J.. Rigidity and non-recurrence along sequences. Ergod. Th. & Dynam. Sys. 34(5) (2014), 1464–1502.Google Scholar
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303, with an appendix by Imre Ruzsa.Google Scholar
Bergelson, V. and McCutcheon, R.. Recurrence for semigroup actions and a non-commutative Schur theorem. Topological Dynamics and Applications (Minneapolis, MN, 1995) (Contemporary Mathematics, 215) . American Mathematical Society, Providence, RI, 1998, pp. 205–222.Google Scholar
Bergelson, V. and Ruzsa, I. Z.. Sumsets in difference sets. Israel J. Math. 174 (2009), 1–18.Google Scholar
Björklund, M. and Fish, A.. Plünnecke inequalities for countable abelian groups. J. Reine Angew. Math. 730 (2017), 199–224.Google Scholar
Boshernitzan, M., Kolesnik, G., Quas, A. and Wierdl, M.. Ergodic averaging sequences. J. Anal. Math. 95 (2005), 63–103.Google Scholar
Cornfeld, I. P., Fomin, S. V. and Sinaĭ, Ya. G.. Ergodic Theory (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 245) . Springer, New York, 1982, translated from the Russian by A. B. Sosinskiĭ.Google Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View towards Number Theory (Graduate Texts in Mathematics, 259) . Springer, London, 2011.Google Scholar
Fayad, B. and Kanigowski, A.. Rigidity times for a weakly mixing dynamical system which are not rigidity times for any irrational rotation. Ergod. Th. & Dynam. Sys. 35(8) (2015), 2529–2534.Google Scholar
Forrest, A. H.. Recurrence in dynamical systems: a combinatorial approach. PhD Thesis, Ohio State University, ProQuest LLC, Ann Arbor, MI, 1990.Google Scholar
Forrest, A. H.. The construction of a set of recurrence which is not a set of strong recurrence. Israel J. Math. 76(1–2) (1991), 215–228.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (M. B. Porter Lectures) . Princeton University Press, Princeton, NJ, 1981.Google Scholar
Geroldinger, A. and Ruzsa, I. Z.. Combinatorial number theory and additive group theory. Advanced Courses in Mathematics. CRM Barcelona. Birkhäuser Verlag, Basel, 2009, Courses and seminars from the DocCourse in Combinatorics and Geometry held in Barcelona, 2008.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Graham, C. C. and Carruth McGehee, O.. Essays in Commutative Harmonic Analysis (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Science], 238) . Springer, New York, Berlin, 1979.Google Scholar
Griesmer, J. T.. Sumsets of dense sets and sparse sets. Israel J. Math. 190 (2012), 229–252.Google Scholar
Griesmer, J. T.. Bohr topology and difference sets for some abelian groups. ArXiv e-prints, 2016,arXiv:1608.01014.Google Scholar
Griesmer, J. T.. Single recurrence in abelian groups. ArXiv e-prints, 2017, arXiv:1701.00465.Google Scholar
Hegyvári, N. and Ruzsa, I. Z.. Additive structure of difference sets and a theorem of Følner. Australas. J. Combin. 64 (2016), 437–443.Google Scholar
Hewitt, E. and Kakutani, S.. A class of multiplicative linear functionals on the measure algebra of a locally compact Abelian group. Illinois J. Math. 4 (1960), 553–574.Google Scholar
Jewett, R. I.. The prevalence of uniquely ergodic systems. J. Math. Mech. 19 (1969/1970), 717–729.Google Scholar
Katznelson, Y.. Sequences of integers dense in the Bohr group. Proc. Roy. Inst. of Tech. (June, 1973), 79–86.Google Scholar
Krieger, W.. On unique ergodicity. Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability (University of California, Berkeley, CA, 1970/1971) (Vol. II: Probability Theory) . University of California Press, Berkeley, CA, 1972, pp. 327–346.Google Scholar
McCutcheon, R.. Three results in recurrence. Ergodic Theory and its Connections with Harmonic Analysis (Alexandria, 1993) (London Mathematical Society Lecture Note Series, 205) . Cambridge University Press, Cambridge, 1995, pp. 349–358.Google Scholar
McCutcheon, R.. Elemental Methods in Ergodic Ramsey Theory (Lecture Notes in Mathematics, 1722) . Springer, Berlin, 1999.Google Scholar
McDiarmid, C.. On the method of bounded differences. Surveys in Combinatorics, 1989 (Norwich, 1989) (London Mathematical Society Lecture Note Series, 141) . Cambridge University Press, Cambridge, 1989, pp. 148–188.Google Scholar
Petersen, K.. Ergodic Theory (Cambridge Studies in Advanced Mathematics, 2) . Cambridge University Press, Cambridge, 1989, corrected reprint of the 1983 original.Google Scholar
Rudin, W.. Fourier Analysis on Groups (Interscience Tracts in Pure and Applied Mathematics, 12) . Interscience Publishers, New York, 1962.Google Scholar
Saeki, S.. Bohr compactification and continuous measures. Proc. Amer. Math. Soc. 80(2) (1980), 244–246.Google Scholar
Umoh, H.. Maximal density ideal of 𝛽S . Math. Japon. 42(2) (1995), 245–247.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar
Wolf, J.. The structure of popular difference sets. Israel J. Math. 179 (2010), 253–278.Google Scholar