Published online by Cambridge University Press: 05 April 2018
We study the action of the affine group 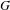 $G$ of
$G$ of 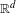 $\mathbb{R}^{d}$ on the space
$\mathbb{R}^{d}$ on the space  $X_{k,\,d}$ of
$X_{k,\,d}$ of 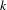 $k$-dimensional affine subspaces. Given a compactly supported Zariski dense probability measure
$k$-dimensional affine subspaces. Given a compactly supported Zariski dense probability measure  $\unicode[STIX]{x1D707}$ on
$\unicode[STIX]{x1D707}$ on 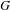 $G$, we show that
$G$, we show that 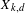 $X_{k,d}$ supports a
$X_{k,d}$ supports a  $\unicode[STIX]{x1D707}$-stationary measure
$\unicode[STIX]{x1D707}$-stationary measure  $\unicode[STIX]{x1D708}$ if and only if the
$\unicode[STIX]{x1D708}$ if and only if the 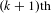 $(k+1)\text{th}$ Lyapunov exponent of
$(k+1)\text{th}$ Lyapunov exponent of  $\unicode[STIX]{x1D707}$ is strictly negative. In particular, when
$\unicode[STIX]{x1D707}$ is strictly negative. In particular, when  $\unicode[STIX]{x1D707}$ is symmetric,
$\unicode[STIX]{x1D707}$ is symmetric,  $\unicode[STIX]{x1D708}$ exists if and only if
$\unicode[STIX]{x1D708}$ exists if and only if  $2k\geq d$.
$2k\geq d$.