Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:38:02.414Z Has data issue: false hasContentIssue false
  • English
  • Français

Recognizability for sequences of morphisms

Published online by Cambridge University Press:  24 January 2018

VALÉRIE BERTHÉ ,
WOLFGANG STEINER ,
JÖRG M. THUSWALDNER  and
REEM YASSAWI
VALÉRIE BERTHÉ
Affiliation:
IRIF, CNRS UMR 8243, Université Paris Diderot – Paris 7, Case 7014, 75205 Paris Cedex 13, France email [email protected], [email protected]
WOLFGANG STEINER
Affiliation:
IRIF, CNRS UMR 8243, Université Paris Diderot – Paris 7, Case 7014, 75205 Paris Cedex 13, France email [email protected], [email protected]
JÖRG M. THUSWALDNER
Affiliation:
Chair of Mathematics and Statistics, University of Leoben, A-8700 Leoben, Austria email [email protected]
REEM YASSAWI
Affiliation:
ICJ, CNRS UMR 5208, Université Claude Bernard Lyon 1, F-69622 Villeurbanne Cedex, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate different notions of recognizability for a free monoid morphism 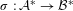$\unicode[STIX]{x1D70E}:{\mathcal{A}}^{\ast }\rightarrow {\mathcal{B}}^{\ast }$. Full recognizability occurs when each (aperiodic) point in 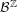${\mathcal{B}}^{\mathbb{Z}}$ admits at most one tiling with words 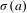$\unicode[STIX]{x1D70E}(a)$, 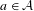$a\in {\mathcal{A}}$. This is stronger than the classical notion of recognizability of a substitution 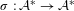$\unicode[STIX]{x1D70E}:{\mathcal{A}}^{\ast }\rightarrow {\mathcal{A}}^{\ast }$, where the tiling must be compatible with the language of the substitution. We show that if 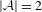$|{\mathcal{A}}|=2$, or if $\unicode[STIX]{x1D70E}$’s incidence matrix has rank 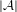$|{\mathcal{A}}|$, or if $\unicode[STIX]{x1D70E}$ is permutative, then $\unicode[STIX]{x1D70E}$ is fully recognizable. Next we investigate the classical notion of recognizability and improve earlier results of Mossé [Puissances de mots et reconnaissabilité des points fixes d’une substitution. Theoret. Comput. Sci.99(2) (1992), 327–334] and Bezuglyi et al [Aperiodic substitution systems and their Bratteli diagrams. Ergod. Th. & Dynam. Sys.29(1) (2009), 37–72], by showing that any substitution is recognizable for aperiodic points in its substitutive shift. Finally we define recognizability and also eventual recognizability for sequences of morphisms which define an $S$-adic shift. We prove that a sequence of morphisms on alphabets of bounded size, such that compositions of consecutive morphisms are growing on all letters, is eventually recognizable for aperiodic points. We provide examples of eventually recognizable, but not recognizable, sequences of morphisms, and sequences of morphisms which are not eventually recognizable. As an application, for a recognizable sequence of morphisms, we obtain an almost everywhere bijective correspondence between the $S$-adic shift it generates, and the measurable Bratteli–Vershik dynamical system that it defines.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 11 , November 2019 , pp. 2896 - 2931
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almeida, J. and Costa, A.. Presentations of Schützenberger groups of minimal subshifts. Israel J. Math. 196(1) (2013), 1–31.10.1007/s11856-012-0139-4Google Scholar
Arnoux, P. and Fisher, A. M.. The scenery flow for geometric structures on the torus: the linear setting. Chin. Ann. Math. Ser. B 22(4) (2001), 427–470.Google Scholar
Adams, T., Ferenczi, S. and Petersen, K.. Constructive symbolic presentations of rank one measure-preserving systems. Colloq. Math. 150(2) (2017), 243–255.10.4064/cm7124-3-2017Google Scholar
Anderson, J. E. and Putnam, I. F.. Topological invariants for substitution tilings and their associated C ∗ -algebras. Ergod. Th. & Dynam. Sys. 18(3) (1998), 509–537.Google Scholar
Arnoux, P. and Rauzy, G.. Représentation géométrique de suites de complexité 2n + 1. Bull. Soc. Math. France 119(2) (1991), 199–215.10.24033/bsmf.2164Google Scholar
Andress, T. I. and Robinson, E. A. Jr. The Cech cohomology and the spectrum for 1-dimensional tiling systems. Ergodic Theory, Dynamical Systems, and the Continuing Influence of John C. Oxtoby (Contemporary Mathematics, 678) . American Mathematical Society, Providence, RI, 2016, pp. 53–71.Google Scholar
Aubrun, N. and Sablik, M.. Multidimensional effective S-adic subshifts are sofic. Unif. Distrib. Theory 9(2) (2014), 7–29.Google Scholar
Berthé, V. and Delecroix, V.. Beyond substitutive dynamical systems: S-adic expansions. RIMS Lecture note ‘Kôkyûroku Bessatsu’ B46 (2014), 81–123.Google Scholar
Berthé, V., De Felice, C., Dolce, F., Leroy, J., Perrin, D., Reutenauer, C. and Rindone, G.. Maximal bifix decoding. Discrete Math. 338(5) (2015), 725–742.Google Scholar
Berthé, V.. Multidimensional Euclidean algorithms, numeration and substitutions. Integers 11B (2011), A2.Google Scholar
Berthé, V., Ferenczi, S. and Zamboni, L. Q.. Interactions between dynamics, arithmetics and combinatorics: the good, the bad, and the ugly. Algebraic and Topological Dynamics (Contemporary Mathematics, 385) . American Mathematical Society, Providence, RI, 2005, pp. 333–364.10.1090/conm/385/07205Google Scholar
Bédaride, N., Hubert, P. and Leplaideur, R.. Thermodynamic formalism and substitutions. Preprint, 2015, arXiv:1511.03322v1.Google Scholar
Bezuglyi, S., Kwiatkowski, J. and Medynets, K.. Aperiodic substitution systems and their Bratteli diagrams. Ergod. Th. & Dynam. Sys. 29(1) (2009), 37–72.Google Scholar
Bezuglyi, S., Kwiatkowski, J., Medynets, K. and Solomyak, B.. Invariant measures on stationary Bratteli diagrams. Ergod. Th. & Dynam. Sys. 30(4) (2010), 973–1007.Google Scholar
Boyland, P. and Severa, W.. Geometric representation of the infixmax S-adic family. Fund. Math. 240(1) (2018), 15–50.10.4064/fm258-12-2016Google Scholar
Berthé, V., Steiner, W. and Thuswaldner, J. M.. Geometry, dynamics and arithmetic of $S$ -adic shifts. Preprint, 2014, arXiv:1410.0331v3.Google Scholar
Cassaigne, J.. An algorithm to test if a given circular HD0L-language avoids a pattern. Information Processing ’94 (Hamburg, 1994, IFIP Trans. A Comput. Sci. Tech., A-51, I) . North-Holland, Amsterdam, 1994, pp. 459–464.Google Scholar
Crabb, M. J., Duncan, J. and McGregor, C. M.. Finiteness and recognizability problems for substitution maps on two symbols. Semigroup Forum 81(1) (2010), 71–84.Google Scholar
Cassaigne, J., Ferenczi, S. and Messaoudi, A.. Weak mixing and eigenvalues for Arnoux–Rauzy sequences. Ann. Inst. Fourier (Grenoble) 58(6) (2008), 1983–2005.Google Scholar
Cassaigne, J., Ferenczi, S. and Zamboni, L. Q.. Imbalances in Arnoux–Rauzy sequences. Ann. Inst. Fourier (Grenoble) 50(4) (2000), 1265–1276.10.5802/aif.1792Google Scholar
Canterini, V. and Siegel, A.. Automate des préfixes-suffixes associé à une substitution primitive. J. Théor. Nombres Bordeaux 13(2) (2001), 353–369.Google Scholar
Canterini, V. and Siegel, A.. Geometric representation of substitutions of Pisot type. Trans. Amer. Math. Soc. 353(12) (2001), 5121–5144.Google Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S.. On automorphism groups of low complexity subshifts. Ergod. Th. & Dynam. Sys. 36(1) (2016), 64–95.10.1017/etds.2015.70Google Scholar
Durand, F., Host, B. and Skau, C.. Substitutional dynamical systems, Bratteli diagrams and dimension groups. Ergod. Th. & Dynam. Sys. 19(4) (1999), 953–993.Google Scholar
Durand, F. and Leroy, J.. S-adic conjecture and Bratteli diagrams. C. R. Math. Acad. Sci. Paris 350(21–22) (2012), 979–983.Google Scholar
Durand, F. and Leroy, J.. The constant of recognizability is computable for primitive morphisms. J. Integer Seq. 20(4) (2017), 15, Art. 17.4.54.Google Scholar
Downarowicz, T. and Maass, A.. Finite-rank Bratteli–Vershik diagrams are expansive. Ergod. Th. & Dynam. Sys. 28(3) (2008), 739–747.Google Scholar
Durand, F.. Corrigendum and addendum to: ‘Linearly recurrent subshifts have a finite number of non-periodic subshift factors’ [Ergod. Th. & Dynam. Sys. 20(4) (2000), 1061–1078]. Ergod. Th. & Dynam. Sys. 23 (2003), 663–669.Google Scholar
Emme, J.. Thermodynamic formalism and k-bonacci substitutions. Discrete Contin. Dyn. Syst. 37(7) (2017), 3701–3719.Google Scholar
Ferenczi, S.. Rank and symbolic complexity. Ergod. Th. & Dynam. Sys. 16(4) (1996), 663–682.Google Scholar
Ferenczi, S.. Systems of finite rank. Colloq. Math. 73(1) (1997), 35–65.Google Scholar
Fisher, A. M.. Nonstationary mixing and the unique ergodicity of adic transformations. Stoch. Dyn. 9(3) (2009), 335–391.Google Scholar
Frick, S., Petersen, K. and Shields, S.. Dynamical properties of some adic systems with arbitrary orderings. Ergod. Th. & Dynam. Sys. 37(7) (2017), 2131–2162.Google Scholar
Priebe Frank, N. and Sadun, L.. Fusion: a general framework for hierarchical tilings of ℝ d . Geom. Dedicata 171 (2014), 49–186.Google Scholar
Fine, N. J. and Wilf, H. S.. Uniqueness theorems for periodic functions. Proc. Amer. Math. Soc. 16 (1965), 109–114.Google Scholar
Host, B.. Valeurs propres des systèmes dynamiques définis par des substitutions de longueur variable. Ergod. Th. & Dynam. Sys. 6(4) (1986), 529–540.Google Scholar
Høynes, S.-M.. Finite-rank Bratteli–Vershik diagrams are expansive—a new proof. Math. Scand. 120(2) (2017), 195–210.10.7146/math.scand.a-25613Google Scholar
Holton, C., Radin, C. and Sadun, L.. Conjugacies for tiling dynamical systems. Comm. Math. Phys. 254(2) (2005), 343–359.Google Scholar
Janssen, J., Quas, A. and Yassawi, R.. Bratteli diagrams where random orders are imperfect. Proc. Amer. Math. Soc. 145(2) (2017), 721–735.10.1090/proc/13284Google Scholar
Klouda, K. and Starosta, Š.. Characterization of circular D0L-systems. Preprint, 2014, arXiv:1401.0038.Google Scholar
Martin, J. C.. Minimal flows arising from substitutions of non-constant length. Math. Syst. Theory 7 (1973), 72–82.Google Scholar
Medynets, K.. Cantor aperiodic systems and Bratteli diagrams. C. R. Math. Acad. Sci. Paris 342(1) (2006), 43–46.10.1016/j.crma.2005.10.024Google Scholar
Marmi, S., Moussa, P. and Yoccoz, J.-C.. The cohomological equation for Roth-type interval exchange maps. J. Amer. Math. Soc. 18(4) (2005), 823–872.Google Scholar
Mossé, B.. Puissances de mots et reconnaissabilité des points fixes d’une substitution. Theoret. Comput. Sci. 99(2) (1992), 327–334.10.1016/0304-3975(92)90357-LGoogle Scholar
Mossé, B.. Reconnaissabilité des substitutions et complexité des suites automatiques. Bull. Soc. Math. France 124(2) (1996), 329–346.Google Scholar
Mignosi, F. and Séébold, P.. If a DOL language is k-power free then it is circular. Automata, Languages and Programming (Lund, 1993) (Lecture Notes in Computer Science, 700) . Springer, Berlin, 1993, pp. 507–518.Google Scholar
Queffélec, M.. Substitution Dynamical Systems—Spectral Analysis (Lecture Notes in Mathematics, 1294) , 2nd edn. Springer, Berlin, 2010.Google Scholar
Solomyak, B.. Nonperiodicity implies unique composition for self-similar translationally finite tilings. Discrete Comput. Geom. 20(2) (1998), 265–279.Google Scholar
Vershik, A. M.. A theorem on the Markov periodical approximation in ergodic theory. J. Sov. Math. 28 (1985), 667–674.Google Scholar
Vershik, A. M. and Livshits, A. N.. Adic models of ergodic transformations, spectral theory, substitutions, and related topics. Representation Theory and Dynamical Systems (Advances in Soviet Mathematics, 9) . American Mathematical Society, Providence, RI, 1992, pp. 185–204.Google Scholar
Zorich, A.. Finite Gauss measure on the space of interval exchange transformations. Lyapunov exponents. Ann. Inst. Fourier (Grenoble) 46(2) (1996), 325–370.Google Scholar