Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T00:35:49.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Real-analytic weak mixing diffeomorphisms preserving a measurable Riemannian metric

Published online by Cambridge University Press:  05 July 2016

PHILIPP KUNDE
PHILIPP KUNDE*
Affiliation:
Department of Mathematics, University of Hamburg, Bundesstrasse 55, Hamburg, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

On the torus $\mathbb{T}^{m}$ of dimension 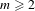$m\geq 2$ we prove the existence of a real-analytic weak mixing diffeomorphism preserving a measurable Riemannian metric. The proof is based on a real-analytic version of the approximation by conjugation method with explicitly defined conjugation maps and partition elements.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 5 , August 2017 , pp. 1547 - 1569
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anosov, D. V. and Katok, A.. New examples in smooth ergodic theory. Ergodic diffeomorphisms. Tr. Mosk. Mat. Obs. 23 (1970), 3–36.Google Scholar
Banerjee, S.. Non-standard real-analytic realizations of some rotations of the circle. Ergod. Th. & Dynam. Sys. accepted. Preprint, 2015, arXiv:1501.01531.Google Scholar
Benhenda, M.. Non-standard smooth realization of shifts on the torus. J. Mod. Dyn. 7(3) (2013), 329–367.Google Scholar
Fayad, B. and Katok, A.. Constructions in elliptic dynamics. Ergod. Th. & Dynam. Sys. 24(5) (2004), 1477–1520.Google Scholar
Fayad, B. and Katok, A.. Analytic uniquely ergodic volume preserving maps on odd spheres. Comment. Math. Helv. 89(N4) (2014), 963–977.CrossRefGoogle Scholar
Fayad, B. and Saprykina, M.. Weak mixing disc and annulus diffeomorphisms with arbitrary Liouville rotation number on the boundary. Ann. Sci. Éc. Norm. Supér. (4) 38(3) (2005), 339–364.CrossRefGoogle Scholar
Fayad, B., Saprykina, M. and Windsor, A.. Nonstandard smooth realizations of Liouville rotations. Ergod. Th. & Dynam. Sys. 27 (2007), 1803–1818.Google Scholar
Gunesch, R. and Katok, A.. Construction of weakly mixing diffeomorphisms preserving measurable Riemannian metric and smooth measure. Discrete Contin. Dyn. Syst. 6 (2000), 61–88.Google Scholar
Gunesch, R. and Kunde, P.. Weakly mixing diffeomorphisms preserving a measurable Riemannian metric are dense in ${\mathcal{A}}_{\unicode[STIX]{x1D6FC}}\left(M\right)$ for arbitrary Liouvillean number $\unicode[STIX]{x1D6FC}$ . Preprint, 2015, arXiv:1512.00075.Google Scholar
Halmos, P. R.. Measure Theory. Van Nostrand, Princeton, NJ, 1965.Google Scholar
Kunde, P.. Uniform rigidity sequences for weak mixing diffeomorphisms on D2 , A and T2 . J. Math. Anal. Appl. 429 (2015), 111–130.Google Scholar
Saprykina, M.. Analytic non-linearizable uniquely ergodic diffeomorphisms on T2 . Ergod. Th. & Dynam. Sys. 23 (2003), 935–955.Google Scholar
Sklover, M. D.. Classical dynamical systems on the torus with continuous spectrum. Izv. Vyssh. Uchebn. Zaved. Mat. 10 (1967), 113–124.Google Scholar