Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T00:50:46.082Z Has data issue: false hasContentIssue false
  • English
  • Français

Rationally almost periodic sequences, polynomial multiple recurrence and symbolic dynamics

Published online by Cambridge University Press:  18 January 2018

V. BERGELSON ,
J. KUŁAGA-PRZYMUS ,
M. LEMAŃCZYK  and
F. K. RICHTER
V. BERGELSON
Affiliation:
Department of Mathematics, Ohio State University, Columbus, OH 43210, USA email [email protected], [email protected]
J. KUŁAGA-PRZYMUS
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Chopina 12/18, 87-100 Toruń, Poland email [email protected], [email protected]
M. LEMAŃCZYK
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Chopina 12/18, 87-100 Toruń, Poland email [email protected], [email protected]
F. K. RICHTER
Affiliation:
Department of Mathematics, Ohio State University, Columbus, OH 43210, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A set 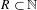$R\subset \mathbb{N}$ is called rational if it is well approximable by finite unions of arithmetic progressions, meaning that for every 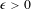$\unicode[STIX]{x1D716}>0$ there exists a set 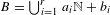$B=\bigcup _{i=1}^{r}a_{i}\mathbb{N}+b_{i}$, where 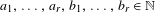$a_{1},\ldots ,a_{r},b_{1},\ldots ,b_{r}\in \mathbb{N}$, such that

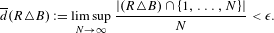$$\begin{eqnarray}\overline{d}(R\triangle B):=\limsup _{N\rightarrow \infty }\frac{|(R\triangle B)\cap \{1,\ldots ,N\}|}{N}<\unicode[STIX]{x1D716}.\end{eqnarray}$$
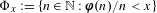Examples of rational sets include many classical sets of number-theoretical origin such as the set of squarefree numbers, the set of abundant numbers, or sets of the form $\unicode[STIX]{x1D6F7}_{x}:=\{n\in \mathbb{N}:\boldsymbol{\unicode[STIX]{x1D711}}(n)/n<x\}$, where 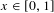$x\in [0,1]$ and 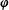$\boldsymbol{\unicode[STIX]{x1D711}}$ is Euler’s totient function. We investigate the combinatorial and dynamical properties of rational sets and obtain new results in ergodic Ramsey theory. Among other things, we show that if 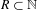$R\subset \mathbb{N}$ is a rational set with 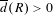$\overline{d}(R)>0$, then the following are equivalent:

(a) 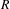$R$ is divisible, i.e. 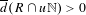$\overline{d}(R\cap u\mathbb{N})>0$ for all 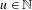$u\in \mathbb{N}$;

(b) 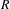$R$ is an averaging set of polynomial single recurrence;

(c) 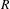$R$ is an averaging set of polynomial multiple recurrence.

As an application, we show that if 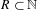$R\subset \mathbb{N}$ is rational and divisible, then for any set 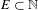$E\subset \mathbb{N}$ with 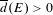$\overline{d}(E)>0$ and any polynomials 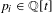$p_{i}\in \mathbb{Q}[t]$, 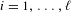$i=1,\ldots ,\ell$, which satisfy 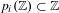$p_{i}(\mathbb{Z})\subset \mathbb{Z}$ and 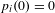$p_{i}(0)=0$ for all 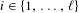$i\in \{1,\ldots ,\ell \}$, there exists 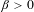$\unicode[STIX]{x1D6FD}>0$ such that the set

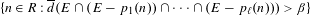$$\begin{eqnarray}\{n\in R:\overline{d}(E\cap (E-p_{1}(n))\cap \cdots \cap (E-p_{\ell }(n)))>\unicode[STIX]{x1D6FD}\}\end{eqnarray}$$
has positive lower density.

Ramsey-theoretical applications naturally lead to problems in symbolic dynamics, which involve rationally almost periodic sequences (sequences whose level-sets are rational). We prove that if 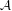${\mathcal{A}}$ is a finite alphabet, 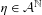$\unicode[STIX]{x1D702}\in {\mathcal{A}}^{\mathbb{N}}$ is rationally almost periodic, $S$ denotes the left-shift on 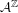${\mathcal{A}}^{\mathbb{Z}}$ and

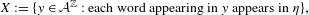$$\begin{eqnarray}X:=\{y\in {\mathcal{A}}^{\mathbb{Z}}:\text{each word appearing in}~y~\text{appears in}~\unicode[STIX]{x1D702}\},\end{eqnarray}$$
then $\unicode[STIX]{x1D702}$ is a generic point for an $S$-invariant probability measure $\unicode[STIX]{x1D708}$ on 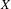$X$ such that the measure-preserving system 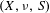$(X,\unicode[STIX]{x1D708},S)$ is ergodic and has rational discrete spectrum.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 9 , September 2019 , pp. 2332 - 2383
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allouche, J.-P.. The number of factors in a paperfolding sequence. Bull. Aust. Math. Soc. 46 (1992), 23–32.Google Scholar
Allouche, J.-P. and Shallit, J.. Automatic Sequences: Theory, Applications, Generalizations. Cambridge University Press, Cambridge, 2003.Google Scholar
Auslander, L., Green, L. and Hahn, F.. Flows on Homogeneous Spaces (Annals of Mathematics Studies, 53) . Princeton University Press, Princeton, NJ, 1963, with the assistance of L. Markus and W. Massey, and an appendix by L. Greenberg.Google Scholar
Bartnicka, A., Kasjan, S., Kułaga-Przymus, J. and Lemańczyk, M.. $\mathscr{B}$ -free sets and dynamics. Trans. Amer. Math. Soc., to appear, doi:10.1090/tran/7132.Google Scholar
Beiglböck, M., Bergelson, V., Hindman, N. and Strauss, D.. Multiplicative structures in additively large sets. J. Combin. Theory Ser. A 113 (2006), 1219–1242.Google Scholar
Bellow, A. and Losert, V.. The weighted pointwise ergodic theorem and the individual ergodic theorem along subsequences. Trans. Amer. Math. Soc. 288 (1985), 307–345.Google Scholar
Bergelson, V.. Sets of recurrence of Z m -actions and properties of sets of differences in Z m . J. Lond. Math. Soc. (2) 31 (1985), 295–304.Google Scholar
Bergelson, V.. Ergodic Ramsey theory. Logic and Combinatorics (Arcata, CA, 1985) (Contemporary Mathematics, 65) . American Mathematical Society, Providence, RI, 1987, pp. 63–87.Google Scholar
Bergelson, V.. Ergodic Ramsey theory – an update. Ergodic Theory of Z d Actions (Warwick, 1993–1994) (London Mathematical Society Lecture Note Series, 228) . Cambridge University Press, Cambridge, 1996, pp. 1–61.Google Scholar
Bergelson, V. and Håland, I. J.. Sets of recurrence and generalized polynomials. Convergence in Ergodic Theory and Probability (Columbus, OH, 1993) (Ohio State University Mathematics Research Institute Publications, 5) . De Gruyter, Berlin, 1996, pp. 91–110.Google Scholar
Bergelson, V., Host, B., McCutcheon, R. and Parreau, F.. Aspects of uniformity in recurrence. Colloq. Math. 84/85 (2000), 549–576.Google Scholar
Bergelson, V. and Leibman, A.. Polynomial extensions of van der Waerden’s and Szemerédi’s theorems. J. Amer. Math. Soc. 9 (1996), 725–753.Google Scholar
Bergelson, V. and Ruzsa, I.. Squarefree numbers, IP sets and ergodic theory. Paul Erdős and His Mathematics, I (Budapest, 1999) (Bolyai Society Mathematical Studies, 11) . János Bolyai Mathematical Socety, Budapest, 2002, pp. 147–160.Google Scholar
Berstel, J., Perrin, D. and Reutenauer, C.. Codes and Automata (Encyclopedia of Mathematics and its Applications, 129) . Cambridge University Press, Cambridge, 2010.Google Scholar
Besicovitch, A. S.. On the density of certain sequences of integers. Math. Ann. 110 (1935), 336–341.Google Scholar
Besicovitch, A. S.. Almost Periodic Functions. Dover Publications, New York, 1955.Google Scholar
Cellarosi, F. and Sinai, Y. G.. Ergodic properties of square-free numbers. J. Eur. Math. Soc. (JEMS) 15 (2013), 1343–1374.Google Scholar
Chowla, S.. The Riemann Hypothesis and Hilbert’s Tenth Problem (Mathematics and Its Applications, 4) . Gordon and Breach Science Publishers, New York, 1965.Google Scholar
Davenport, H.. Über numeri abundantes. Sitzungsber. Preuss. Akad. Wiss.,Phys.-Math. Kl. 6 (1933), 830–837.Google Scholar
Davenport, H. and Erdős, P.. On sequences of positive integers. Acta Arith. 2 (1936), 147–151.Google Scholar
Davenport, H. and Erdős, P.. On sequences of positive integers. J. Indian Math. Soc. (N.S.) 15 (1951), 19–24.Google Scholar
Dekking, M., Mendès France, M. and van der Poorten, A.. Folds. Math. Intelligencer 4 (1982), 130–138.Google Scholar
Deshouillers, J.-M., Drmota, M. and Müllner, C.. Automatic sequences generated by synchronizing automata fulfill the Sarnak conjecture. Studia Math. 231 (2015), 83–95.Google Scholar
Downarowicz, T.. Survey of odometers and Toeplitz flows. Algebraic and Topological Dynamics (Contemporary Mathematics, 385) . American Mathematical Society, Providence, RI, 2005, pp. 7–37.Google Scholar
Downarowicz, T.. Entropy in Dynamical Systems (New Mathematical Monographs, 18) . Cambridge University Press, Cambridge, 2011.Google Scholar
Downarowicz, T. and Iwanik, A.. Quasi-uniform convergence in compact dynamical systems. Studia Math. 89 (1988), 11–25.Google Scholar
El Abdalaoui, E., Kułaga-Przymus, J., Lemańczyk, M. and De La Rue, T.. The Chowla and the Sarnak conjectures from ergodic theory point of view. Discrete Contin. Dyn. Syst. 37(6) (2017), 2899–2944.Google Scholar
El Abdalaoui, E., Lemańczyk, M. and de la Rue, T.. A dynamical point of view on the set of ℬ-free integers. Int. Math. Res. Not. IMRN 2015 (2015), 7258–7286.Google Scholar
Frantzikinakis, N.. Multiple ergodic averages for three polynomials and applications. Trans. Amer. Math. Soc. 360 (2008), 5435–5475.Google Scholar
Frantzikinakis, N., Host, B. and Kra, B.. The polynomial multidimensional Szemerédi theorem along shifted primes. Israel J. Math. 194 (2013), 331–348.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory 1 (1967), 1–49.Google Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (M. B. Porter Lectures) . Princeton University Press, Princeton, NJ, 1981.Google Scholar
Hahn, F. and Parry, W.. Some characteristic properties of dynamical systems with quasi-discrete spectra. Math. Systems Theory 2 (1968), 179–190.Google Scholar
Hall, R. R.. Sets of Multiples (Cambridge Tracts in Mathematics, 118) . Cambridge University Press, Cambridge, 1996.Google Scholar
Hindman, N.. Ultrafilters and combinatorial number theory. Number Rheory, Carbondale 1979 (Proc. Southern Illinois Conf., Southern Illinois Univ., Carbondale, IL, 1979) (Lecture Notes in Mathematics, 751) . Springer, Berlin, 1979, pp. 119–184.Google Scholar
Hornfeck, B.. Zur Dichte der Menge der vollkommenen Zahlen. Arch. Math. (Basel) 6 (1955), 442–443.Google Scholar
Host, B. and Kra, B.. Convergence of polynomial ergodic averages. Israel J. Math. 149 (2005), 1–19.Google Scholar
Iwanik, A.. Weyl almost periodic points in topological dynamics. Colloq. Math. 56 (1988), 107–119.Google Scholar
Jacobs, K. and Keane, M.. 0–1-sequences of Toeplitz type. Z. Wahrscheinlichkeitstheorie Verw. Gebiete 13 (1969), 123–131.Google Scholar
Keane, M.. Generalized Morse sequences. Z. Wahrscheinlichkeitstheorie Verw. Gebiete 10 (1968), 335–353.Google Scholar
Kryloff, N. and Bogoliouboff, N.. La théorie générale de la mesure dans son application à l’étude des systèmes dynamiques de la mécanique non linéaire. Ann. of Math. (2) 38 (1937), 65–113.Google Scholar
Kułaga-Przymus, J., Lemańczyk, M. and Weiss, B.. On invariant measures for ℬ-free systems. Proc. Lond. Math. Soc. (3) 110 (2015), 1435–1474.Google Scholar
Lehrer, E.. Topological mixing and uniquely ergodic systems. Israel J. Math. 57 (1987), 239–255.Google Scholar
Leibman, A.. Convergence of multiple ergodic averages along polynomials of several variables. Israel J. Math. 146 (2005), 303–315.Google Scholar
Leibman, A.. Pointwise convergence of ergodic averages for polynomial sequences of translations on a nilmanifold. Ergod. Th. & Dynam. Syst. 25 (2005), 201–213.Google Scholar
Leibman, A.. Multiple polynomial correlation sequences and nilsequences. Ergod. Th. & Dynam. Syst. 30 (2010), 841–854.Google Scholar
Matomäki, K. and Radziwiłł, M.. Multiplicative functions in short intervals. Ann. of Math. (2) 183 (2016), 1015–1056.Google Scholar
Matomäki, K., Radziwiłł, M. and Tao, T.. An averaged form of Chowla’s conjecture. Algebra Number Theory 9 (2015), 2167–2196.Google Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics. Amer. J. Math. 60 (1938), 815–866.Google Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.Google Scholar
Parry, W.. Ergodic properties of affine transformations and flows on nilmanifolds. Amer. J. Math. 91 (1969), 757–771.Google Scholar
Peckner, R.. Uniqueness of the measure of maximal entropy for the squarefree flow. Israel J. Math. 210 (2015), 335–357.Google Scholar
Petersen, K.. Ergodic Theory (Cambridge Studies in Advanced Mathematics, 2) . Cambridge University Press, Cambridge, 1983.Google Scholar
Queffélec, M.. Substitution Dynamical Systems—Spectral Analysis (Lecture Notes in Mathematics, 1294) . 2nd edn. Springer, Berlin, 2010.Google Scholar
Sarnak, P.. Three lectures on the Möbius function, randomness and dynamics. http://publications.ias.edu/sarnak/.Google Scholar
Schoenberg, I.. Über die asymptotische Verteilung reeller Zahlen mod 1. Math. Z. 28 (1928), 171–199.Google Scholar
Szemerédi, E.. On sets of integers containing no k elements in arithmetic progression. Acta Arith. 27 (1975), 199–245.Google Scholar
Thue, A.. Über unendliche Zeichenreihen. Nor. Vid. Selsk. Skr. I Math-Nat. Kl. 7 (1906).Google Scholar
Thue, A.. Die Lösung eines Spezialfalles eines generellen logischen Problems. Nor. Vid. Selsk. Skr. I Math-Nat. Kl. Chris. 8 (1910).Google Scholar
Walsh, M. N.. Norm convergence of nilpotent ergodic averages. Ann. of Math. (2) 175 (2012), 1667–1688.Google Scholar
Wang, Z.. Möbius disjointness for analytic skew products. Invent. Math. 209 (2017), 175–196.Google Scholar
Weiss, B.. Single Orbit Dynamics (CBMS Regional Conference Series in Mathematics, 95) . American Mathematical Society, Providence, RI, 2000.Google Scholar