Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-25T19:32:36.389Z Has data issue: false hasContentIssue false
  • English
  • Français

Rank-one systems, flexible classes and Shannon orbit equivalence

Part of: Ergodic theory

Published online by Cambridge University Press:  23 December 2024

CORENTIN CORREIA
CORENTIN CORREIA*
Affiliation:
Université Paris Cité, Paris 75006, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We build a Shannon orbit equivalence between the universal odometer and a variety of rank-one systems. This is done in a unified manner using what we call flexible classes of rank-one transformations. Our main result is that every flexible class contains an element which is Shannon orbit equivalent to the universal odometer. Since a typical example of flexible class is 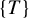$\{T\}$ when T is an odometer, our work generalizes a recent result by Kerr and Li, stating that every odometer is Shannon orbit equivalent to the universal odometer. When the flexible class is a singleton, the rank-one transformation given by the main result is explicit. This applies to odometers and Chacon’s map. We also prove that strongly mixing systems, systems with a given eigenvalue, or irrational rotations whose angle belongs to any fixed non-empty open subset of the real line form flexible classes. In particular, strong mixing, rationality or irrationality of the eigenvalues are not preserved under Shannon orbit equivalence.

Keywords

orbit equivalencerank-one systemsodometerspoint spectrummixing properties

MSC classification

Primary: 37A35: Entropy and other invariants, isomorphism, classification
Secondary: 37A20: Orbit equivalence, cocycles, ergodic equivalence relations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 51
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Austin, T.. Behaviour of entropy under bounded and integrable orbit equivalence. Geom. Funct. Anal. 26(6) (2016), 1483–1525.CrossRefGoogle Scholar
Belinskaya, R. M.. Partitions of Lebesgue space in trajectories defined by ergodic automorphisms. Funct. Anal. Appl. 2(3) (1969), 190–199.CrossRefGoogle Scholar
Chacon, R. V.. Weakly mixing transformations which are not strongly mixing. Proc. Amer. Math. Soc. 22(3) (1969), 559–562.CrossRefGoogle Scholar
Carderi, A., Joseph, M., Le Maître, F. and Tessera, R.. Belinskaya’s theorem is optimal. Fund. Math. 263(1) (2023), 51–90.CrossRefGoogle Scholar
Drillick, H., Espinosa-Dominguez, A., Jones-Baro, J. N., Leng, J., Mandelshtam, Y. and Silva, C. E.. Non-rigid rank-one infinite measures on the circle. Dyn. Syst. 38(2) (2023), 275–300.CrossRefGoogle Scholar
Downarowicz, T.. Entropy in Dynamical Systems (New Mathematical Monographs, 18). Cambridge University Press, Cambridge, 2011.CrossRefGoogle Scholar
Danilenko, A. I. and Vieprik, M. I.. Explicit rank-1 constructions for irrational rotations. Studia Math. 270(2) (2023), 121–144.CrossRefGoogle Scholar
Dye, H. A.. On groups of measure preserving transformations. I. Amer. J. Math. 81(1) (1959), 119–159.CrossRefGoogle Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory: With a View Towards Number Theory. Springer, London, 2011.CrossRefGoogle Scholar
Ferenczi, S.. Systems of finite rank. Colloq. Math. 73(1) (1997), 35–65.CrossRefGoogle Scholar
Foreman, M., Rudolph, D. and Weiss, B.. The conjugacy problem in ergodic theory. Ann. of Math. (2) 173(3) (2011), 1529–1586.CrossRefGoogle Scholar
Gao, S. and Ziegler, C.. Topological mixing properties of rank-one subshifts. Trans. London Math. Soc. 6(1) (2019), 1–21.CrossRefGoogle Scholar
Halmos, P. R. and Von Neumann, J.. Operator methods in classical mechanics. II. Ann. of Math. (2) 43(2) (1942), 332–350.CrossRefGoogle Scholar
Del Junco, A.. Transformations with discrete spectrum are stacking transformations. Canad. J. Math. 28(4) (1976), 836–839.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Ergodic Theory: Independence and Dichotomies (Springer Monographs in Mathematics). Springer International Publishing, Cham, 2017.Google Scholar
Kerr, D. and Li, H.. Entropy, Shannon orbit equivalence, and sparse connectivity. Math. Ann. 380(3) (2021), 1497–1562.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Entropy, virtual Abelianness and Shannon orbit equivalence. Ergod. Th. & Dynam. Sys.. Published online 10 April 2024.Google Scholar
Ornstein, D.. Bernoulli shifts with the same entropy are isomorphic. Adv. Math. 4(3) (1970), 337–352.CrossRefGoogle Scholar
Ornstein, D. S.. On the root problem in ergodic theory. Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, Volume 2: Probability Theory. Vol. 6.2. Ed. L. M. Le Cam, J. Neyman and E. L. Scott. University of California Press, Berkeley, CA, 1972, pp. 347–357.Google Scholar
Ornstein, D. S., Rudolph, D. J. and Weiss, B.. Equivalence of measure preserving transformations. Mem. Amer. Math. Soc. 37(262) (1982), xii+116 pp.Google Scholar
Ornstein, D. S. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48(1) (1987), 1–141.CrossRefGoogle Scholar
Viana, M. and Oliveira, K.. Foundations of Ergodic Theory (Cambridge Studies in Advanced Mathematics, 151). Cambridge University Press, Cambridge, 2016.Google Scholar