Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:37:43.700Z Has data issue: false hasContentIssue false
  • English
  • Français

Range-renewal structure in continued fractions

Published online by Cambridge University Press:  08 March 2016

JUN WU  and
JIAN-SHENG XIE
JUN WU
Affiliation:
Department of Mathematics, Huazhong University of Science and Technology, Wuhan 430074, PR China email [email protected]
JIAN-SHENG XIE
Affiliation:
School of Mathematical Sciences, Fudan University, Shanghai 200433, PR China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 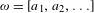$\unicode[STIX]{x1D714}=[a_{1},a_{2},\ldots ]$ be the infinite expansion of a continued fraction for an irrational number 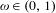$\unicode[STIX]{x1D714}\in (0,1)$, and let 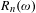$R_{n}(\unicode[STIX]{x1D714})$ (respectively, 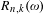$R_{n,k}(\unicode[STIX]{x1D714})$, 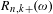$R_{n,k+}(\unicode[STIX]{x1D714})$) be the number of distinct partial quotients, each of which appears at least once (respectively, exactly 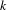$k$ times, at least 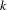$k$ times) in the sequence 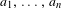$a_{1},\ldots ,a_{n}$. In this paper, it is proved that, for Lebesgue almost all 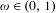$\unicode[STIX]{x1D714}\in (0,1)$ and all 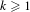$k\geq 1$,

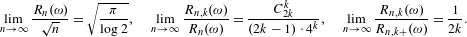$$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }\frac{R_{n}(\unicode[STIX]{x1D714})}{\sqrt{n}}=\sqrt{\frac{\unicode[STIX]{x1D70B}}{\log 2}},\quad \lim _{n\rightarrow \infty }\frac{R_{n,k}(\unicode[STIX]{x1D714})}{R_{n}(\unicode[STIX]{x1D714})}=\frac{C_{2k}^{k}}{(2k-1)\cdot 4^{k}},\quad \lim _{n\rightarrow \infty }\frac{R_{n,k}(\unicode[STIX]{x1D714})}{R_{n,k+}(\unicode[STIX]{x1D714})}=\frac{1}{2k}.\end{eqnarray}$$
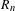The Hausdorff dimensions of certain level sets about $R_{n}$ are discussed.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 4 , June 2017 , pp. 1323 - 1344
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Billingsley, P.. Ergodic Theory and Information. John Wiley, New York, 1965.Google Scholar
Chen, X.-X., Xie, J.-S. and Ying, J.-G.. Range-renewal processes: SLLN, power law and beyonds. Preprint, 2013, arXiv:1305.1829.Google Scholar
Derriennic, Y.. Quelques applications du théorème ergodique sous-additif. Conference on Random Walks (Kleebach, 1979) (French) (Astérisque, 74) . Société Mathématique de France, Paris, 1980, pp. 183–201; 4, (French. English summary).Google Scholar
Dvoretzky, A. and Erdös, P.. Some problems on random walk in space. Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, 1950. University of California Press, Berkeley and Los Angeles, 1951, pp. 353–367.Google Scholar
Erdös, P. and Taylor, S. J.. Some problems concerning the structure of random walk paths. Acta Math. Acad. Sci. Hungar. 11 (1960), 137–162.Google Scholar
Good, I. J.. The fractional dimensional theory of continued fractions. Proc. Cambridge Philos. Soc. 37 (1941), 199–228.CrossRefGoogle Scholar
Hirst, K. E.. A problem in the fractional dimension theory of continued fractions. Quart. J. Math. Oxford Ser. 21 (1970), 29–35.Google Scholar
Hua, S., Rao, H., Wen, Z.-Y. and Wu, J.. On the structures and dimensions of Moran sets. Sci. China Ser. A 43(8) (2000), 836–852.CrossRefGoogle Scholar
Iosifescu, M. and Kraaikamp, C.. Metrical Theory of Continued Fractions (Mathematics and its Applications, 547) . Kluwer Academic Publishers, Dordrecht, 2002.Google Scholar
Jarník, V.. Zur Metrischen Theorie der Diophantischen Approximationen. Prace Mat.-Fiz. 36 (1928–1929), 91–106.Google Scholar
Khintchine, A. Ya.. Continued Fractions. Translated by Peter Wynn. P. Noordhoff, Ltd., Groningen, 1963, pp. iii+101.Google Scholar
Khintchine, A. Ya.. Continued Fractions. The University of Chicago Press, Chicago, 1964, pp. xi+95.Google Scholar
Kingman, J. F. C.. The ergodic theory of subadditive stochastic processes. J. Roy. Statist. Soc. Ser. B 30 (1968), 499–510.Google Scholar
Kingman, J. F. C.. Subadditive ergodic theory. Ann. Probab. 1 (1973), 883–909.CrossRefGoogle Scholar
Kingman, J. F. C.. Subadditive processes. École d’Été de Probabilités de Saint-Flour, V-1975 (Lecture Notes in Mathematics, 539) . Springer, Berlin, 1976, pp. 167–223.Google Scholar
Kuzmin, R. O.. On a problem of Gauss. Dokl. Akad. Nauk SSSR A (1928), 375–380 (in Russian); French version in Atti Congr. Internaz. Mat. (Bologna, 1928), Zanichelli, Bologna, 1932, Tomo VI, pp. 83–89.Google Scholar
Lévy, P.. Sur les lois de probabilité dont dépendent les quotient complets et incomplets d’une fraction continue. Bull. Soc. Math. France 57 (1929), 178–194.CrossRefGoogle Scholar
Lévy, P.. Théorie de l’addition des variables aléatoires, 2ème édition. Gauthier-Villars, Paris, 1937 (1ère édition).Google Scholar
Li, B., Wang, B.-W., Wu, J. and Xu, J.. The shrinking target problem in the dynamical system of continued fractions. Proc. Lond. Math. Soc. (3) 108(1) (2014), 159–186.Google Scholar
Lúczak, T.. On the fractional dimension of sets of continued fractions. Mathematika 44(1) (1997), 50–53.CrossRefGoogle Scholar
Mauldin, R. D. and Urbański, M.. Dimensions and measures in infinite iterated function systems. Proc. Lond. Math. Soc. 73 (1996), 105–154.CrossRefGoogle Scholar
Mauldin, R. D. and Urbański, M.. Conformal iterated function systems with applications to the geometry of continued fractions. Trans. Amer. Math. Soc. 351(12) (1999), 4995–5025.Google Scholar
Pollicott, M. and Weiss, H.. Multifractal analysis of Lyapunov exponent for continued fraction and Manneville–Pomeau transformations and applications to Diophantine approximation. Comm. Math. Phys. 207 (1999), 145–171.CrossRefGoogle Scholar
Rempe-Gillen, L. and Urbański, M.. Non-autonomous conformal iterated function systems and Moran-set constructions. Preprint, 2012, arXiv:1210.7469, Trans. Amer. Math. Soc., to appear.Google Scholar
Revesz, P.. Random Walk in Random and Non-Random Environments, 2nd edn. World Scientific, Hackensack, NJ, 2005, pp. xvi+380.Google Scholar
Szűsz, P.. Über einen Kusminschen Statz. Acta Math. Acad. Sci. Hungar. 12 (1961), 447–453.Google Scholar
Wang, B.-W. and Wu, J.. Hausdorff dimension of certain sets arising in continued fraction expansions. Adv. Math. 218 (2008), 1319–1339.Google Scholar
Wen, Z.-Y.. Moran sets and Moran classes. Chinese Sci. Bull. 46(22) (2001), 1849–1856.CrossRefGoogle Scholar
Wirsing, E.. On the theorem of Gauss–Kusmin–Lévy and a Frobenius type theorem for function spaces. Acta Arith. 24 (1973–1974), 507–528.Google Scholar
Wu, J.. A remark on the growth of the denominators of convergents. Monatsh. Math. 147 (2006), 259–264.Google Scholar
Xie, J.-S. and Xu, Y.-Y.. Range-renewal structure of transient simple random walk. Statist. Probab. Lett. 83(10) (2013), 2220–2221.Google Scholar