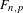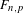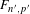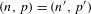Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Balankin, Alexander S.
2017.
The topological Hausdorff dimension and transport properties of Sierpiński carpets.
Physics Letters A,
Vol. 381,
Issue. 34,
p.
2801.
RAO, FENG
and
WEN, SHENGYOU
2018.
REMARKS ON QUASISYMMETRIC RIGIDITY OF SQUARE SIERPIŃSKI CARPETS.
Fractals,
Vol. 26,
Issue. 05,
p.
1850060.
Wang, Haihang
Xu, He
Zhang, Yonghui
Chen, Siqing
Zhao, Zitong
and
Chen, Junlong
2019.
Design of a Bio-Inspired Anti-Erosion Structure for a Water Hydraulic Valve Core: An Experimental Study.
Biomimetics,
Vol. 4,
Issue. 3,
p.
63.
Fu, Yuming
and
Yang, Fei
2020.
Area and Hausdorff dimension of Sierpiński carpet Julia sets.
Mathematische Zeitschrift,
Vol. 294,
Issue. 3-4,
p.
1441.
RAO, FENG
and
WEN, FAN
2024.
Quasisymmetrically rigid self-similar carpets.
Ergodic Theory and Dynamical Systems,
p.
1.
Sheng, Yahui
Wei, Chun
and
Wen, Fan
2024.
Note on quasisymmetric rigidity of carpets.
Topology and its Applications,
Vol. 353,
Issue. ,
p.
108960.