Published online by Cambridge University Press: 30 September 2021
Two given orbits of a minimal circle homeomorphism f are said to be geometrically equivalent if there exists a quasisymmetric circle homeomorphism identifying both orbits and commuting with f. By a well-known theorem due to Herman and Yoccoz, if f is a smooth diffeomorphism with Diophantine rotation number, then any two orbits are geometrically equivalent. It follows from the a priori bounds of Herman and Świątek, that the same holds if f is a critical circle map with rotation number of bounded type. By contrast, we prove in the present paper that if f is a critical circle map whose rotation number belongs to a certain full Lebesgue measure set in
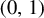 $(0,1)$
, then the number of equivalence classes is uncountable (Theorem 1.1). The proof of this result relies on the ergodicity of a two-dimensional skew product over the Gauss map. As a by-product of our techniques, we construct topological conjugacies between multicritical circle maps which are not quasisymmetric, and we show that this phenomenon is abundant, both from the topological and measure-theoretical viewpoints (Theorems 1.6 and 1.8).
$(0,1)$
, then the number of equivalence classes is uncountable (Theorem 1.1). The proof of this result relies on the ergodicity of a two-dimensional skew product over the Gauss map. As a by-product of our techniques, we construct topological conjugacies between multicritical circle maps which are not quasisymmetric, and we show that this phenomenon is abundant, both from the topological and measure-theoretical viewpoints (Theorems 1.6 and 1.8).