Hostname: page-component-55f67697df-xlmdk Total loading time: 0 Render date: 2025-05-10T01:49:19.265Z Has data issue: false hasContentIssue false
  • English
  • Français

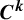Quantitative reducibility of ${\boldsymbol {C}^{\boldsymbol {k}}}$ quasi-periodic cocycles

Part of: Finite-dimensional Hamiltonian, Lagrangian, contact, and nonholonomic systems

Published online by Cambridge University Press:  13 November 2024

AO CAI ,
HUIHUI LV  and
ZHIGUO WANG
AO CAI
Affiliation:
Soochow University School of Mathematical Sciences, Suzhou, Jiangsu, China (e-mail: [email protected], [email protected])
HUIHUI LV*
Affiliation:
Soochow University School of Mathematical Sciences, Suzhou, Jiangsu, China (e-mail: [email protected], [email protected])
ZHIGUO WANG
Affiliation:
Soochow University School of Mathematical Sciences, Suzhou, Jiangsu, China (e-mail: [email protected], [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper establishes an extreme 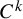$C^k$ reducibility theorem of quasi-periodic 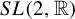$SL(2, \mathbb {R})$ cocycles in the local perturbative region, revealing both the essence of Eliasson [Floquet solutions for the 1-dimensional quasi-periodic Schrödinger equation. Comm. Math. Phys. 146 (1992), 447–482], and Hou and You [Almost reducibility and non-perturbative reducibility of quasi-periodic linear systems. Invent. Math. 190 (2012), 209–260] in respectively the non-resonant and resonant cases. By paralleling further the reducibility process with the almost reducibility, we are able to acquire the least initial regularity as well as the least loss of regularity for the whole Kolmogorov–Arnold–Moser (KAM) iterations. This, in return, makes various spectral applications of quasi-periodic Schrödinger operators wide open.

Keywords

discretefinitely differentiablequantitative reducibilitycocycle

MSC classification

Primary: 37J40: Perturbations, normal forms, small divisors, KAM theory, Arnol'd diffusion
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 45 , Issue 6 , June 2025 , pp. 1649 - 1672
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Asch, J. and Knauf, A.. Motion in periodic potentials. Nonlinearity 11 (1997), 175–200.Google Scholar
Avila, A., Bochi, J. and Damanik, D.. Cantor spectrum for Schrödinger operators with potentials arising from generalized skew-shifts. Duke Math. J. 146 (2009), 253–280.CrossRefGoogle Scholar
Avila, A., Fayad, B. and Krikorian, R.. A KAM scheme for $SL(2, \mathbb{R})$ cocycles with Liouvillean frequencies. Geom. Funct. Anal. 21 (2011), 1001–1019.CrossRefGoogle Scholar
Avila, A. and Jitomirskaya, S.. Almost localization and almost reducibility. J. Eur. Math. Soc. (JEMS) 12 (2010), 93–131.CrossRefGoogle Scholar
Avila, A. and Krikorian, R.. Reducibility or nonuniform hyperbolicity for quasiperiodic Schrödinger cocycles. Ann. of Math. (2) 164 (2006), 911–940.CrossRefGoogle Scholar
Avila, A., Last, Y., Shamis, M. and Zhou, Q.. On the abominable properties of the almost Mathieu operator with well-approximated frequencies. Duke Math. J. 173(4) (2024), 603–672.CrossRefGoogle Scholar
Avron, J. and Simon, B.. Almost periodic Schrödinger operators II. The integrated density of states. Duke Math. J. 50 (1983), 369–291.CrossRefGoogle Scholar
Berti, M. and Biasco, L.. Forced vibrations of wave equations with non-monotone nonlinearities. Ann. Inst. H. Poincaré C Anal. Non Linéaire 23 (2006), 439–474.CrossRefGoogle Scholar
Binder, I., Damanik, D., Goldstein, M. and Lukic, M.. Almost periodicity in time of solutions of the KdV equation. Duke Math. J. 167 (2018), 2633–2678.Google Scholar
Cai, A.. The absolutely continuous spectrum of finitely differentiable quasi-periodic Schrödinger operators. Ann. Henri Poincaré 23 (2022), 4195–4226.CrossRefGoogle Scholar
Cai, A., Chavaudret, C., You, J. and Zhou, Q.. Sharp Hölder continuity of the Lyapunov exponent of finitely differentiable quasi-periodic cocycles. Math. Z. 291 (2019), 931–958.CrossRefGoogle Scholar
Cai, A. and Ge, L.. Reducibility of finitely differentiable quasi-periodic cocycles and its spectral applications. J. Dynam. Differential Equations 34 (2022), 2079–2104.CrossRefGoogle Scholar
Cai, A. and Wang, X.. Polynomial decay of the gap length for ${\mathrm{C}}^{\mathrm{K}}$ quasi-periodic Schrödinger operators and spectral application. J. Funct. Anal. 281 (2021), 109035.CrossRefGoogle Scholar
Chavaudret, C.. Strong almost reducibility for analytic and Gevrey quasi-periodic cocycles. Soc. Math. France 141 (2013), 47–106.CrossRefGoogle Scholar
Combes, J.-M.. Connections between quantum dynamics and spectral properties of time-evolution operators. Differ. Equ. Appl. Math. Phys. 192 (1993), 59–68.Google Scholar
Damanik, D.. Schrödinger operators with dynamically defined potentials. Ergod. Th. & Dynam. Sys. 37 (2017), 1681–1764.CrossRefGoogle Scholar
Damanik, D. and Fillman, J.. One-Dimensional Ergodic Schrödinger Operators: I. General Theory (Graduate Studies in Mathematics, 221). American Mathematical Society, Providence, RI, 2022.CrossRefGoogle Scholar
Damanik, D., Goldstein, M. and Lukic, M.. The spectrum of a Schrödinger operator with small quasi-periodic potential is homogeneous. J. Spectr. Theory 6 (2016), 415–427.CrossRefGoogle Scholar
Damanik, D., Goldstein, M. and Lukic, M.. The isospectral torus of quasi-periodic Schrödinger operators via periodic approximations. Invent. Math. 207 (2017), 895–980.CrossRefGoogle Scholar
Damanik, D., Lukic, M. and Yessen, W.. Quantum dynamics of periodic and limit-periodic Jacobi and block Jacobi matrices with applications to some quantum many body problems. Comm. Math. Phys. 337 (2015), 1535–1561.CrossRefGoogle Scholar
Deimling, K.. Nonlinear functional analysis. Bull. Amer. Math. Soc. (N.S.) 20 (1989), 277–280.Google Scholar
Dinaburg, E. I. and Sinai, Y. G.. The one-dimensional Schrödinger equation with a quasiperiodic potential. Funct. Anal. Appl. 9 (1975), 279–289.CrossRefGoogle Scholar
Eliasson, L. H.. Floquet solutions for the 1-dimensional quasi-periodic Schrödinger equation. Comm. Math. Phys. 146 (1992), 447–482.CrossRefGoogle Scholar
Fillman, J.. Ballistic transport for limit-periodic Jacobi matrices with applications to quantum many-body problems. Comm. Math. Phys. 350 (2017), 1275–1297.CrossRefGoogle Scholar
Ge, L. and Kachkovskiy, I.. Ballistic transport for one-dimensional quasiperiodic Schrödinger operators. Comm. Pure Appl. Math. 76 (2023), 2577–2612.CrossRefGoogle Scholar
Hou, X. and You, J.. Almost reducibility and non-perturbative reducibility of quasi-periodic linear systems. Invent. Math. 190 (2012), 209–260.CrossRefGoogle Scholar
Jian, W. and Shi, Y.. Sharp Hölder continuity of the integrated density of states for extended harper’s model with a Liouville frequency. Acta Math. Sci. 39 (2019), 1240–1254.CrossRefGoogle Scholar
Johnson, R. and Moser, J.. The rotation number for almost periodic potentials. Comm. Math. Phys. 84 (1982), 403–438.CrossRefGoogle Scholar
Johnson, R. A.. Exponential dichotomy, rotation number and linear differential operators with bounded coefficients. J. Differential Equations 61 (1986), 54–78.CrossRefGoogle Scholar
Last, Y.. Quantum dynamics and decompositions of singular continuous spectra. J. Funct. Anal. 142 (1996), 406–445.CrossRefGoogle Scholar
Leguil, M., You, J., Zhao, Z. and Zhou, Q.. Asymptotics of spectral gaps of quasi-periodic Schrödinger operators. Preprint, 2017, arXiv:1712.04700.Google Scholar
Moser, J. and Pöschel, J.. An extension of a result by Dinaburg and Sinai on quasi-periodic potentials. Comment. Math. Helv. 59 (1984), 39–85.CrossRefGoogle Scholar
Puig, J.. A nonperturbative Eliasson’s reducibility theorem. Nonlinearity 19 (2005), 355.CrossRefGoogle Scholar
Simon, B.. Absence of ballistic motion. Comm. Math. Phys. 134 (1990), 209–212.CrossRefGoogle Scholar
Sodin, M. and Yuditskii, P.. Almost periodic Sturm–Liouville operators with Cantor homogeneous spectrum. Comment. Math. Helv. 70 (1995), 639–658.CrossRefGoogle Scholar
Sodin, M. and Yuditskii, P.. Almost periodic Jacobi matrices with homogeneous spectrum, infinite dimensional Jacobi inversion, and hardy spaces of character-automorphic functions. J. Geom. Anal. 7 (1997), 387–435.CrossRefGoogle Scholar
Wang, Y. and Zhang, Z.. Cantor spectrum for a class of quasi-periodic Schrödinger operators. Int. Math. Res. Not. IMRN 2017 (2017), 2300–2336.Google Scholar
You, J.. Quantitative almost reducibility and its applications. Proc. Int. Congr. Math. 4 (2018), 2113–2135.Google Scholar
Young, G.. Ballistic transport for limit-periodic Schrödinger operators in one dimension. J. Spectr. Theory 13 (2021), 451–489.CrossRefGoogle Scholar
Zehnder, E.. Generalized implicit function theorems with applications to some small divisor problems. Comm. Pure Appl. Math. 28 (1975), 91–140.CrossRefGoogle Scholar
Zhao, Z.. Ballistic motion in one-dimensional quasi-periodic discrete Schrödinger equation. Comm. Math. Phys. 347 (2016), 511–549.CrossRefGoogle Scholar
Zhao, Z. and Zhang, Z.. Ballistic transport and absolute continuity of one-frequency Schrodinger operators. Comm. Math. Phys. 351 (2017), 877–921.Google Scholar