Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T03:09:00.098Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantitative norm convergence of double ergodic averages associated with two commuting group actions

Published online by Cambridge University Press:  06 November 2014

VJEKOSLAV KOVAČ
VJEKOSLAV KOVAČ*
Affiliation:
Department of Mathematics, University of Zagreb, Bijenička cesta 30, 10000 Zagreb, Croatia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study double averages along orbits for measure-preserving actions of 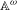$\mathbb{A}^{{\it\omega}}$, the direct sum of countably many copies of a finite abelian group 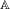$\mathbb{A}$. We show an 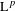$\text{L}^{p}$ norm-variation estimate for these averages, which in particular re-proves their convergence in 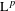$\text{L}^{p}$ for any finite 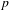$p$ and for any choice of two 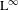$\text{L}^{\infty }$ functions. The result is motivated by recent questions on quantifying convergence of multiple ergodic averages.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 3 , May 2016 , pp. 860 - 874
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Austin, T.. On the norm convergence of non-conventional ergodic averages. Ergodic Th. & Dynam. Sys. 30(2) (2010), 321–338.Google Scholar
Avigad, J. and Rute, J.. Oscillation and the mean ergodic theorem for uniformly convex Banach spaces. Ergodic Th. & Dynam. Sys., to appear, available at arXiv:1203.4124 [math.DS].Google Scholar
Bergelson, V., McCutcheon, R. and Zhang, Q.. A Roth theorem for amenable groups. Amer. J. Math. 119(6) (1997), 1173–1211.CrossRefGoogle Scholar
Bergelson, V., Tao, T. and Ziegler, T.. Multiple recurrence and convergence results associated to Fp𝜔 -actions. J. Anal. Math., to appear, available at arXiv:1305.4717 [math.DS].Google Scholar
Bergh, J. and Löfström, J.. Interpolation Spaces, An Introduction. Springer, New York, 1976.Google Scholar
Bourgain, J.. Double recurrence and almost sure convergence. J. Reine Angew. Math. 404 (1990), 140–161.Google Scholar
Calderón, A. P.. Ergodic theory and translation-invariant operators. Proc. Natl Acad. Sci. USA 59 (1968), 349–353.Google Scholar
Conze, J.-P. and Lesigne, E.. Théorèmes ergodiques pour des mesures diagonales. Bull. Soc. Math. France 112(2) (1984), 143–175.Google Scholar
Demeter, C.. Pointwise convergence of the ergodic bilinear Hilbert transform. Illinois J. Math. 51(4) (2007), 1123–1158.Google Scholar
Demeter, C. and Thiele, C.. On the two-dimensional bilinear Hilbert transform. Amer. J. Math. 132(1) (2010), 201–256.Google Scholar
Do, Y., Oberlin, R. and Palsson, E. A.. Variational bounds for a dyadic model of the bilinear Hilbert transform. Illinois J. Math. 57(1) (2013), 105–119.Google Scholar
Følner, E.. On groups with full Banach mean value. Math. Scand. 3 (1955), 243–254.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.Google Scholar
Furstenberg, H. and Katznelson, Y.. An ergodic Szemerédi theorem for commuting transformations. J. Anal. Math. 34 (1978), 275–291.Google Scholar
Jones, R. L., Kaufman, R., Rosenblatt, J. M. and Wierdl, M.. Oscillation in ergodic theory. Ergodic Th. & Dynam. Sys. 18(4) (1998), 889–935.Google Scholar
Jones, R. L., Ostrovskii, I. V. and Rosenblatt, J. M.. Square functions in ergodic theory. Ergodic Th. & Dynam. Sys. 16(2) (1996), 267–305.CrossRefGoogle Scholar
Kovač, V.. Bellman function technique for multilinear estimates and an application to generalized paraproducts. Indiana Univ. Math. J. 60(3) (2011), 813–846.Google Scholar
Kovač, V.. Boundedness of the twisted paraproduct. Rev. Mat. Iberoam. 28(4) (2012), 1143–1164.Google Scholar
Kovač, V. and Thiele, C.. A T(1) theorem for entangled multilinear dyadic Calderón–Zygmund operators. Illinois J. Math., to appear, available at arXiv:1305.4752 [math.CA].Google Scholar
Lindenstrauss, E.. Pointwise theorems for amenable groups. Invent. Math. 146(2) (2001), 259–295.CrossRefGoogle Scholar
Muscalu, C., Tao, T. and Thiele, C.. A Carleson type theorem for a Cantor group model of the scattering transform. Nonlinearity 16(1) (2003), 219–246.CrossRefGoogle Scholar
Tao, T.. Norm convergence of multiple ergodic averages for commuting transformations. Ergodic Th. & Dynam. Sys. 28(2) (2008), 657–688.Google Scholar
Varadarajan, V. S.. Groups of automorphisms of Borel spaces. Trans. Amer. Math. Soc. 109 (1963), 191–220.Google Scholar
von Neumann, J.. Proof of the quasi-ergodic hypothesis. Proc. Natl Acad. Sci. USA 18 (1932), 70–82.Google Scholar
Walsh, J. L.. A closed set of normal orthogonal functions. Amer. J. Math. 45(1) (1923), 5–24.Google Scholar
Walsh, M. N.. Norm convergence of nilpotent ergodic averages. Ann. of Math. (2) 175(3) (2012), 1667–1688.Google Scholar
Zorin-Kranich, P.. Norm convergence of multiple ergodic averages on amenable groups. J. Anal. Math., to appear, available at arXiv:1111.7292 [math.DS].Google Scholar