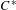Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-19T22:59:54.412Z Has data issue: false hasContentIssue false
  • English
  • Français

Purely infinite labeled graph $C^{\ast }$-algebras

Published online by Cambridge University Press:  04 December 2017

JA A JEONG ,
EUN JI KANG  and
GI HYUN PARK
JA A JEONG
Affiliation:
Department of Mathematical Sciences and Research Institute of Mathematics, Seoul National University, Seoul 08826, Korea email [email protected]
EUN JI KANG
Affiliation:
BK21 Plus Mathematical Sciences Division, Seoul National University, Seoul 08826, Korea email [email protected]
GI HYUN PARK
Affiliation:
Department of Financial Mathematics, Hanshin University, Osan 18101, Korea email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider pure infiniteness of generalized Cuntz–Krieger algebras associated to labeled spaces 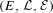$(E,{\mathcal{L}},{\mathcal{E}})$. It is shown that a 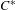$C^{\ast }$-algebra 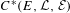$C^{\ast }(E,{\mathcal{L}},{\mathcal{E}})$ is purely infinite in the sense that every non-zero hereditary subalgebra contains an infinite projection (we call this property (IH)) if 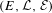$(E,{\mathcal{L}},{\mathcal{E}})$ is disagreeable and every vertex connects to a loop. We also prove that under the condition analogous to (K) for usual graphs, 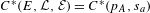$C^{\ast }(E,{\mathcal{L}},{\mathcal{E}})=C^{\ast }(p_{A},s_{a})$ is purely infinite in the sense of Kirchberg and Rørdam if and only if every generating projection 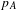$p_{A}$, 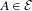$A\in {\mathcal{E}}$, is properly infinite, and also if and only if every quotient of 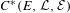$C^{\ast }(E,{\mathcal{L}},{\mathcal{E}})$ has property (IH).

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 8 , August 2019 , pp. 2128 - 2158
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman-Delaroche, C.. Purely infinite C ∗ -algebras arising from dynamical systems. Bull. Soc. Math. France 125 (1997), 199–225.Google Scholar
Bates, T., Carlsen, T. M. and Pask, D.. C ∗ -algebras of labelled graphs III—K-theory computations. Ergod. Th. & Dynam. Sys. 37 (2017), 337–368.Google Scholar
Bates, T., Hong, J. H., Raeburn, I. and Szymanski, W.. The ideal structure of the C ∗ -algebras of infinite graphs. Illinois J. Math. 46 (2002), 1159–1176.Google Scholar
Bates, T. and Pask, D.. C ∗ -algebras of labelled graphs. J. Operator Theory 57 (2007), 101–120.Google Scholar
Bates, T. and Pask, D.. C ∗ -algebras of labelled graphs II—Simplicity results. Math. Scand. 104(2) (2009), 249–274.Google Scholar
Bates, T., Pask, D., Raeburn, I. and Szymanski, W.. The C ∗ -algebras of row-finite graphs. New York J. Math. 6 (2000), 307–324.Google Scholar
Brown, J., Clark, L. and Seirakowski, A.. Purely infinite C ∗ -algebras associated to étale groupoids. Ergod. Th. & Dynam. Sys. 35 (2015), 2397–2411.Google Scholar
Brown, J. H., Clark, L. O., Sierakowski, A. and Sims, A.. Purely infinite simple C ∗ -algebras that are principal groupoid C ∗ -algebras. J. Math. Anal. Appl. 439 (2016), 213–234.Google Scholar
Carlsen, T. M., Ortega, E. and Pardo, E.. C ∗ -algebras associated to Boolean dynamical systems. J. Math. Anal. Appl. 450 (2017), 727–768.Google Scholar
Drinen, D. and Tomforde, M.. The C ∗ -algebras of arbitrary graphs. Rocky Mountain J. Math. 35 (2005), 105–135.Google Scholar
Exel, R.. Inverse semigroups and combinatorial C ∗ -algebras. Bull. Braz. Math. Soc. (N.S.) 39 (2008), 191–313.Google Scholar
Exel, R. and Pardo, E.. The tight groupoid of an inverse semigroup. Semigroup Forum 92 (2016), 274–303.Google Scholar
Fujii, M. and Watatani, Y.. Cuntz–Krieger algebras associated with adjoint graphs. Math. Japan 25 (1980), 501–506.Google Scholar
Gelfond, A.. Sur les nombres qui ont des propriétés additives et multiplicatives données. Acta Arith. 13 (1968), 259–265.Google Scholar
Gottschalk, W. H. and Hedlund, G. A.. A characterization of the Morse minimal set. Proc. Amer. Math. Soc. 15 (1964), 70–74.Google Scholar
Hjelmborg, J.. Purely infinite and stable C ∗ -algebras of graphs and dynamical systems. Ergod. Th. & Dynam. Sys. 21 (2001), 1789–1808.Google Scholar
Hong, J. H. and Szymanski, W.. Purely infinite Cuntz–Krieger algebras of directed graphs. Bull. Lond. Math. Soc. (5) 35 (2003), 689–696.Google Scholar
Jeong, J. A., Kang, E. J. and Kim, S. H.. AF labeled graph C ∗ -algebras. J. Funct. Anal. 266 (2014), 2153–2173.Google Scholar
Jeong, J. A., Kang, E. J., Kim, S. H. and Park, G. H.. Finite simple labeled graph C ∗ -algebras of Cantor minimal subshifts. J. Math. Anal. App. 446 (2017), 395–410.Google Scholar
Jeong, J. A. and Kim, S. H.. On simple labeled graph C ∗ -algebras. J. Math. Anal. Appl. 386 (2012), 631–640.Google Scholar
Jeong, J. A., Kim, S. H. and Park, G. H.. The structure of gauge-invariant ideals of labeled graph C ∗ -algebras. J. Funct. Anal. 262 (2012), 1759–1780.Google Scholar
Jeong, J. A. and Park, G. H.. Graph C ∗ -algebras of real rank zero. J. Funct. Anal. 188 (2002), 216–226.Google Scholar
Kang, S. and Pask, D.. Aperiodic and primitive ideals of row-finite k-graphs. Internat. J. Math. 25 (2014), 1450022.Google Scholar
Kitchens, B. P.. Symbolic Dynamics. Springer, Berlin, 1998.Google Scholar
Kumjian, A., Pask, D. and Raeburn, I.. Cuntz–Krieger algebras of directed graphs. Pacific J. Math. 184 (1998), 161–174.Google Scholar
Kumjian, A., Pask, D., Raeburn, I. and Renault, J.. Graphs, groupoids, and Cuntz–Krieger algebras. J. Funct. Anal. 144 (1997), 505–541.Google Scholar
Kirchberg, E. and Rørdam, M.. Non-simple purely finite C ∗ -algebras. Amer. J. Math. 122 (2000), 637–666.Google Scholar
Laca, M. and Spielberg, J.. Purely infinite C ∗ -algebras from boundary actions of discrete groups. J. Reine Angew. Math. 480 (1996), 125–139.Google Scholar
Matsumoto, K.. Construction and pure infiniteness of C ∗ -algebras associated with lambda-graph systems. Math. Scan. 97 (2005), 73–88.Google Scholar
Pask, D., Sierakowski, A. and Sims, A.. Real rank and topological dimension of higher rank graph algebras. Preprint, 2015, arXiv:1503.08517v2 [math.OA].Google Scholar
Rørdam, M. and Sierakowski, A.. Purely infinite C ∗ -algebras aring from crossed products. Ergod. Th. & Dynam. Sys. 32 (2012), 273–293.Google Scholar