Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T17:46:11.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Potential kernel, hitting probabilities and distributional asymptotics

Part of: Ergodic theory Limit theorems Stochastic processes Dynamical systems with hyperbolic behavior Markov processes

Published online by Cambridge University Press:  26 January 2019

FRANÇOISE PÈNE  and
DAMIEN THOMINE
FRANÇOISE PÈNE
Affiliation:
Université de Brest and Institut Universitaire de France, Laboratoire de Mathématiques de Bretagne Atlantique, UMR CNRS 6205, 29238 Brest Cedex, France email [email protected]
DAMIEN THOMINE
Affiliation:
Département de Mathématiques d’Orsay, Université Paris-Sud, UMR CNRS 8628, F-91405 Orsay Cedex, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

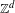$\mathbb{Z}^{d}$-extensions of probability-preserving dynamical systems are themselves dynamical systems preserving an infinite measure, and generalize random walks. Using the method of moments, we prove a generalized central limit theorem for additive functionals of the extension of integral zero, under spectral assumptions. As a corollary, we get the fact that Green–Kubo’s formula is invariant under induction. This allows us to relate the hitting probability of sites with the symmetrized potential kernel, giving an alternative proof and generalizing a theorem of Spitzer. Finally, this relation is used to improve, in turn, the assumptions of the generalized central limit theorem. Applications to Lorentz gases in finite horizon and to the geodesic flow on Abelian covers of compact manifolds of negative curvature are discussed.

Keywords

central limit theoremprobabilistic potential theoryclassical ergodic theoryinfinite measurenull recurrent process

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 60J45: Probabilistic potential theory 60G50: Sums of independent random variables; random walks 37D40: Dynamical systems of geometric origin and hyperbolicity (geodesic and horocycle flows, etc.) 37A05: Measure-preserving transformations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 7 , July 2020 , pp. 1894 - 1967
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory. American Mathematical Society, Providence, RI, 1997.Google Scholar
Aaronson, J. and Denker, M.. Characteristic functions of random variables attracted to 1-stable laws. Ann. Probab. 26(1) (1998), 399–415.Google Scholar
Aaronson, J. and Denker, M.. The Poincaré series of ℂ\backslashℤ. Ergod. Th. & Dynam. Sys. 19(1) (1999), 1–20.Google Scholar
Aaronson, J. and Denker, M.. Local limit theorems for partial sums of stationary sequences generated by Gibbs–Markov maps. Stoch. Dyn. 1 (2001), 193–237.Google Scholar
Aaronson, J. and Zweimüller, R.. Limit theory for some positive stationary processes with infinite mean. Ann. Inst. Henri Poincaré Probab. Stat. 50(1) (2014), 256–284.Google Scholar
Apostol, T. M.. Mathematical Analysis, 2nd edn. Addison-Wesley, Reading, MA, 1974.Google Scholar
Babillot, M. and Ledrappier, F.. Geodesic paths and horocycle flows on Abelian covers. Lie Groups and Ergodic Theory (Mumbai, 1996) (Tata Institute of Fundamental Research Studies in Mathematics, 14). Tata Institute of Fundamental Research, Bombay, 1998, pp. 1–32.Google Scholar
Babillot, M. and Ledrappier, F.. Lalley’s theorem on periodic orbits of hyperbolic flows. Ergod. Th. & Dynam. Sys. 18 (1998), 17–39.Google Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L.. Regular variation. Encyclopedia of Mathematics and its Applications, 27. Cambridge University Press, Cambridge, 1987.Google Scholar
Borodin, A. N.. On the character of convergence to Brownian local time. I. Probab. Theory Related Fields 72(2) (1986), 231–250.Google Scholar
Borodin, A. N.. On the character of convergence to Brownian local time. II. Probab. Theory Related Fields 72(2) (1986), 251–277.Google Scholar
Bowen, R.. Symbolic dynamics for hyperbolic flows. Amer. J. Math. 95 (1973), 429–460.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, Berlin, 1975.Google Scholar
Bunimovich, L. A., Chernov, N. I. and Sinai, Y. G.. Statistical properties of two dimensional hyperbolic billiards. Uspekhi Mat. Nauk 46(4) (1991), 47–106.Google Scholar
Bunimovich, L. A. and Sinai, Y. G.. Statistical properties of Lorentz gas with periodic configuration of scatterers. Comm. Math. Phys. 78 (1981), 479–497.Google Scholar
Chernov, N. and Markarian, R.. Chaotic Billiards (Mathematical Surveys and Monographs, 127). American Mathematical Society, Providence, RI, 2006.Google Scholar
Coelho, Z.. Asymptotic laws for symbolic dynamical systems. Topics in Symbolic Dynamics and Applications (Temuco, 1997) (London Mathematical Society Lecture Note Series, 279). Cambridge University Press, Cambridge, 2000, pp. 123–165.Google Scholar
Csáki, E., Csörgő, M., Földes, A. and Révész, P.. Strong approximation of additive functionals. J. Theoret. Probab. 5(4) (1992), 679–706.Google Scholar
Csáki, E. and Földes, A.. On asymptotic independence and partial sums. Asymptotic Methods in Probability and Statistics, A Volume in Honour of Miklós Csörgõ. North-Holland, Amsterdam, 1998, pp. 373–381.Google Scholar
Csáki, E. and Földes, A.. Asymptotic independence and additive functionals. J. Theoret. Probab. 13(4) (2000), 1123–1144.Google Scholar
Darling, D. A. and Kac, M.. On occupation times for Markoff processes. Trans. Amer. Math. Soc. 84 (1957), 444–458.Google Scholar
Dolgopyat, D., Szász, D. and Varjú, T.. Recurrence properties of Lorentz gas. Duke Math. J. 142 (2008), 241–281.Google Scholar
Dobrushin, R. L.. Two limit theorems for the simplest random walk on a line. Uspekhi Mat. Nauk 10 (1955), 139–146 (in Russian).Google Scholar
Feller, W.. An Introduction to Probability Theory and its Applications, Vol. II. Wiley, New York, 1966.Google Scholar
Galves, A. and Schmitt, B.. Inequalities for hitting times in mixing dynamical systems. Random Comput. Dynam. 5(4) (1997), 337–347.Google Scholar
Gouëzel, S.. Vitesse de décorrélation et théorèmes limites pour les applications non uniformément dilatantes. PhD Thesis, Université Paris XI, 2008 version (in French).Google Scholar
Gouëzel, S.. Almost sure invariance principle for dynamical systems by spectral methods. Ann. Probab. 38(4) (2010), 1639–1671.Google Scholar
Guivarc’h, Y. and Hardy, J.. Théorèmes limites pour une classe de chaînes de Markov et applications aux difféomorphismes d’Anosov. Ann. Inst. Henri Poincaré 24(1) (1988), 73–98 (in French).Google Scholar
Halmos, P. R.. Lectures on ergodic theory. Publications of the Mathematical Society of Japan, Vol. 3. The Mathematical Society of Japan, 1956.Google Scholar
Haydn, N. T. A.. Entry and return times distribution. Dyn. Syst. 28(3) (2013), 333–353.Google Scholar
Hennion, H. and Hervé, L.. Limit Theorems for Markov Chains and Stochastic Properties of Dynamical Systems by Quasi-compactness (Lecture Notes in Mathematics, 1766). Springer, Berlin, 2001.Google Scholar
Hopf, E.. Ergodentheorie. Springer, Berlin, 1937, (in German).Google Scholar
Kac, M.. On the notion of recurrence in discrete stochastic processes. Bull. Amer. Math. Soc. (N.S.) 53 (1947), 1002–1010.Google Scholar
Kakutani, S.. Induced measure preserving transformations. Proc. Imp. Acad. 19 (1943), 635–641.Google Scholar
Karamata, J.. Sur un mode de croissance régulière. Théorèmes fondamentaux. Bull. Soc. Math. France 61 (1933), 55–62 (in French).Google Scholar
Kasahara, Y.. Two limit theorems for occupation times of Markov processes. Jpn. J. Math. 7(2) (1981), 291–300.Google Scholar
Kasahara, Y.. Limit theorems for Lévy processes and Poisson point processes and their applications to Brownian excursions. Publ. Math. Inst. Hautes 24(3) (1984), 521–538.Google Scholar
Kasahara, Y.. A limit theorem for sums of random number of i.i.d. random variables and its application to occupation times of Markov chains. J. Math. Soc. Japan 37(2) (1985), 197–205.Google Scholar
Katsuda, A. and Sunada, T.. Closed orbits in homology classes. Publ. Math. Inst. Hautes Études Sci. 71 (1990), 5–32.Google Scholar
Keller, G. and Liverani, C.. Stability of the spectrum for transfer operators. Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 28 (1999), 141–152.Google Scholar
Kesten, H.. Occupation times for Markov and semi-Markov chains. Trans. Amer. Math. Soc. 103 (1962), 82–112.Google Scholar
Ledrappier, F. and Sarig, O.. Unique ergodicity for non-uniquely ergodic horocycle flows. Discrete Contin. Dyn. Syst. 16 (2006), 411–433.Google Scholar
Ledrappier, F. and Sarig, O.. Invariant measures for the horocycle flow on periodic hyperbolic surfaces. Israel J. Math. 160 (2007), 281–315.Google Scholar
Ledrappier, F. and Sarig, O.. Fluctuations of ergodic sums for horocycle flows on ℤd-covers of finite volume surfaces. Discrete Contin. Dyn. Syst. 22 (2008), 247–325.Google Scholar
Lévy, P.. Sur certains processus stochastiques homogènes. Compos. Math. 7 (1940), 283–339 (in French).Google Scholar
Melbourne, I. and Terhesiu, D.. Operator renewal theory and mixing rates for dynamical systems with infinite measure. Invent. Math. 189(1) (2012), 61–110.Google Scholar
Molchanov, S. A. and Ostrovskii, E.. Symmetric stable processes as traces of degenerate diffusion processes. Teor. Veroyatn. Primen. 14 (1969), 127–130 (in Russian).Google Scholar
Nagaev, S. V.. Some limit theorems for stationary Markov chains. Theory Probab. Appl. 11(4) (1957), 378–406.Google Scholar
Nagaev, S. V.. More exact statements of limit theorems for homogeneous Markov chains. Teor. Veroyatn. Primen. 6 (1961), 67–87 (in Russian).Google Scholar
Paulin, F., Pollicott, M. and Schapira, B.. Equilibrium states in negative curbature. Astérisque 373 (2015), viii+145pp.Google Scholar
Pène, F.. Planar Lorentz process in a random scenery. Ann. Inst. Henri Poincaré Probab. Stat. 45(3) (2009), 818–839.Google Scholar
Pène, F.. Asymptotic of the number of obstacles visited by the planar Lorentz process. Discrete Contin. Dyn. Syst. 24(2) (2009), 567–588.Google Scholar
Pollicott, M. and Sharp, R.. Orbit counting for some discrete groups acting on simply connected manifolds with negative curvature. Invent. Math. 117 (1994), 275–302.Google Scholar
Port, S. C.. Some theorems on functionals of Markov chains. Ann. Math. Statist. 35 (1964), 1275–1290.Google Scholar
Rees, M.. Checking ergodicity of some geodesic flows with infinite Gibbs measure. Ergod. Th. & Dynam. Sys. 1(1) (1981), 107–133.Google Scholar
Sarig, O.. Subexponential decay of correlations. Invent. Math. 150(3) (2002), 629–653.Google Scholar
Saussol, B.. Étude statistique de systèmes dynamiques dilatants. PhD Thesis, Université de Toulon et du Var, 1998 (in French).Google Scholar
Saussol, B.. An introduction to quantitative Poincaré recurrence in dynamical systems. Rev. Math. Phys. 21(8) (2009), 949–979.Google Scholar
Sharp, R.. Closed orbits in homology classes for Anosov flows. Ergod. Th. & Dynam. Sys. 13 (1993), 387–408.Google Scholar
Sinai, Y. G.. Dynamical systems with elastic reflections. Ergodic properties of dispersing billiards. Uspehi Mat. Nauk 25(2) (1970), 141–192 (in Russian).Google Scholar
Spitzer, F.. Principles of Random Walk (Graduate Texts in Mathematics, 34), 2nd edn. Springer, New York, Heidelberg, 1976.Google Scholar
Szász, D. and Varjú, T.. Local limit theorem for the Lorentz process and its recurrence in the plane. Ergod. Th. & Dynam. Sys. 24(1) (2004), 257–278.Google Scholar
Szász, D. and Varjú, T.. Limit laws and recurrence for the planar Lorentz process with infinite horizon. J. Stat. Phys. 129(1) (2007), 59–80.Google Scholar
Thaler, M.. A limit theorem for sojourns near indifferent fixed points of one-dimensional maps. Ergod. Th. & Dynam. Sys. 22(4) (2002), 1289–1312.Google Scholar
Thaler, M. and Zweimüller, R.. Distributional limit theorems in infinite ergodic theory. Probab. Theory Related Fields 135(1) (2006), 15–52.Google Scholar
Thomine, D.. Théorèmes limites pour les sommes de Birkhoff de fonctions d’intégrale nulle en théorie ergodique en mesure infinie. PhD Thesis, Université de Rennes 1, 2013 version (in French).Google Scholar
Thomine, D.. A generalized central limit theorem in infinite ergodic theory. Probab. Theory Related Fields 158(3–4) (2014), 597–636.Google Scholar
Thomine, D.. Variations on a central limit theorem in infinite ergodic theory. Ergod. Th. & Dynam. Sys. 35(5) (2015), 1610–1657.Google Scholar
Thomine, D.. Local time and first return time for periodic semi-flows. Israel J. Math. 215(1) (2016), 53–98.Google Scholar
Young, L.-S.. Statistical properties of dynamical systems with some hyperbolicity. Ann. of Math. (2) 147(3) (1998), 585–650.Google Scholar
Young, L.-S.. Recurrence times and rates of mixing. Israel J. Math. 110 (1999), 153–188.Google Scholar
Zweimüller, R.. Mixing limit theorems for ergodic transformations. J. Theoret. Probab. 20 (2007), 1059–1071.Google Scholar