Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T08:12:47.971Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomial multiple recurrence over rings of integers

Published online by Cambridge University Press:  06 February 2015

VITALY BERGELSON  and
DONALD ROBERTSON
VITALY BERGELSON
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA email [email protected]
DONALD ROBERTSON
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize the polynomial Szemerédi theorem to intersective polynomials over the ring of integers of an algebraic number field, by which we mean polynomials having a common root modulo every ideal. This leads to the existence of new polynomial configurations in positive-density subsets of 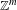$\mathbb{Z}^{m}$ and strengthens and extends recent results of Bergelson, Leibman and Lesigne [Intersective polynomials and the polynomial Szemerédi theorem. Adv. Math.219(1) (2008), 369–388] on polynomials over the integers.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 5 , August 2016 , pp. 1354 - 1378
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergelson, V.. Minimal idempotents and ergodic Ramsey theory. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310) . Cambridge University Press, Cambridge, 2003, pp. 8–39.Google Scholar
Bergelson, V., Furstenberg, H. and McCutcheon, R.. IP-sets and polynomial recurrence. Ergod. Th. & Dynam. Sys. 16(5) (1996), 963–974.Google Scholar
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303, with an appendix by I. Ruzsa.Google Scholar
Bergelson, V. and Leibman, A.. Polynomial extensions of van der Waerden’s and Szemerédi’s theorems. J. Amer. Math. Soc. 9(3) (1996), 725–753.Google Scholar
Bergelson, V., Leibman, A. and Lesigne, E.. Intersective polynomials and the polynomial Szemerédi theorem. Adv. Math. 219(1) (2008), 369–388.Google Scholar
Bergelson, V., Leibman, A. and McCutcheon, R.. Polynomial Szemerédi theorems for countable modules over integral domains and finite fields. J. Anal. Math. 95 (2005), 243–296.Google Scholar
Bergelson, V. and McCutcheon, R.. Uniformity in the polynomial Szemerédi theorem. Ergodic Theory of Z d Actions (Warwick, 1993–1994) (London Mathematical Society Lecture Note Series, 228) . Cambridge University Press, Cambridge, 1996, pp. 273–296.Google Scholar
Bergelson, V. and McCutcheon, R.. An ergodic IP polynomial Szemerédi theorem. Mem. Amer. Math. Soc. 146(695) (2000).Google Scholar
Bergelson, V. and Robertson, D.. Polynomial recurrence with large intersection over countable fields, Preprint, 2014, arXiv:1409.6774 [math.DS].Google Scholar
Borevich, A. I. and Shafarevich, I. R.. Number Theory (Pure and Applied Mathematics, 20) . Academic Press, New York, 1966, pp. x+435 (Translated from the Russian by Newcomb Greenleaf).Google Scholar
Dunford, N. and Schwartz, J. T.. Linear Operators. I. General Theory (Pure and Applied Mathematics, 7) . Interscience Publishers, New York, 1958.Google Scholar
Ellis, R.. Distal transformation groups. Pacific J. Math. 8 (1958), 401–405.Google Scholar
Furstenberg, H., Katznelson, Y. and Ornstein, D.. The ergodic theoretical proof of Szemerédi’s theorem. Bull. Amer. Math. Soc. (N.S.) 7(3) (1982), 527–552.Google Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (M. B. Porter Lectures) . Princeton University Press, Princeton, NJ, 1981.Google Scholar
Furstenberg, H.. Poincaré recurrence and number theory. Bull. Amer. Math. Soc. (N.S.) 5(3) (1981), 211–234.Google Scholar
Furstenberg, H. and Weiss, B.. Topological dynamics and combinatorial number theory. J. Anal. Math. 34 (1978), 61–85 (1979).Google Scholar
Griesmer, J.. Ergodic averages, correlation sequences, and sumsets. PhD Thesis, Ohio State University, Columbus, 2009.Google Scholar
Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 397–488.Google Scholar
Hindman, N. and Strauss, D.. Algebra in the Stone–Čech Compactification (de Gruyter Textbook) , 2nd edn. Walter de Gruyter, Berlin, 2012.Google Scholar
Janusz, G. J.. Algebraic Number Fields (Graduate Studies in Mathematics, 7) , 2nd edn. American Mathematical Society, Providence, RI, 1996.Google Scholar
Keynes, H. B.. Topological dynamics in coset transformation groups. Bull. Amer. Math. Soc. 72 (1966), 1033–1035.Google Scholar
Kamae, T. and Mendès France, M.. Van der Corput’s difference theorem. Israel J. Math. 31(3–4) (1978), 335–342.Google Scholar
Leibman, A.. Convergence of multiple ergodic averages along polynomials of several variables. Israel J. Math. 146 (2005), 303–315.Google Scholar
Leibman, A.. Pointwise convergence of ergodic averages for polynomial actions of ℤ d by translations on a nilmanifold. Ergod. Th. & Dynam. Sys. 25(1) (2005), 215–225.Google Scholar
Leibman, A.. Nilsequences, null-sequences, and multiple correlation sequences. Ergod. Th. & Dynam. Sys. (2014),, doi: 10.1017/etds.2013.36.Google Scholar
Mackey, G. W.. Ergodic transformation groups with a pure point spectrum. Illinois J. Math. 8 (1964), 593–600.Google Scholar
Sárközy, A.. On difference sets of sequences of integers. III. Acta Math. Acad. Sci. Hungar. 31(3–4) (1978), 355–386.Google Scholar
Ziegler, T.. Universal characteristic factors and Furstenberg averages. J. Amer. Math. Soc. 20(1) (2007), 53–97 (electronic).Google Scholar