Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T04:05:52.121Z Has data issue: false hasContentIssue false
  • English
  • Français

The Pisot conjecture for 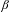$\unicode[STIX]{x1D6FD}$-substitutions

Published online by Cambridge University Press:  22 September 2016

MARCY BARGE
MARCY BARGE*
Affiliation:
Department of Mathematics, Montana State University, Bozeman, MT 59717-0240, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the Pisot conjecture for $\unicode[STIX]{x1D6FD}$-substitutions: if 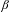$\unicode[STIX]{x1D6FD}$ is a Pisot number, then the tiling dynamical system 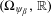$(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}},\mathbb{R})$ associated with the 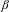$\unicode[STIX]{x1D6FD}$-substitution has pure discrete spectrum. As corollaries: (1) arithmetical coding of the hyperbolic solenoidal automorphism associated with the companion matrix of the minimal polynomial of any Pisot number is almost everywhere one-to-one; and (2) all Pisot numbers are weakly finitary.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 2 , April 2018 , pp. 444 - 472
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akiyama, S.. Cubic Pisot units with finite beta expansions. Algebraic Number Theory and Diophantine Analysis. Eds. Halter-Koch, F. and Tichy, R. F.. de Gruyter, Berlin, New York, 2000, pp. 11–26.Google Scholar
Akiyama, S.. On the boundary of self affine tilings generated by Pisot numbers. J. Math. Soc. Japan 54(2) (2002), 283–308.Google Scholar
Akiyama, S., Barge, M., Berthé, V., Lee, J.-Y. and Siegel, A.. On the Pisot substitution conjecture. Mathematics of Aperiodic Order (Progress in Mathematics, 309) . Eds. Kellendonk, J., Lenz, D. and Savinien, J.. Birkhauser, Basel, 2015, pp. 33–72.Google Scholar
Akiyama, S., Rao, H. and Steiner, W.. A certain finiteness property of Pisot number systems. J. Number Theory 107(1) (2004), 135–160.Google Scholar
Anderson, J. E. and Putnam, I. F.. Topological invariants for substitution tilings and their associated C ∗ -algebras. Ergod. Th. & Dynam. Sys. 18 (1998), 509–537.Google Scholar
Akiyama, S. and Sadahiro, T.. A self-similar tiling generated by the minimal Pisot number. Acta Math. Info. Univ. Ostrav. 6 (1998), 9–26.Google Scholar
Auslander, J.. Minimal Flows and Their Extensions (North-Holland Mathematical Studies, 153) . North-Holland, Amsterdam, 1988.Google Scholar
Baker, V., Barge, M. and Kwapisz, J.. Geometric realization and coincidence for reducible non-unimodular Pisot tiling spaces with an application to 𝛽-shifts. Ann. Inst. Fourier (Grenoble) 56(7) (2006), 2213–2248.Google Scholar
Baake, M. and Lenz, D.. Dynamical systems on translation bounded measures: pure point dynamical and diffraction spectra. Ergod. Th. & Dynam. Sys. 24 (2004), 1867–1893.Google Scholar
Barge, M.. Pure discrete spectrum for a class of one-dimensional tiling systems. Discrete Contin. Dyn. Syst. Ser. A 36(3) (2016), 1159–1173.Google Scholar
Barge, M.. Geometrical and spectral properties of Pisot substitutions. Topology Appl. 205(1) (2016), 28–46.Google Scholar
Barge, M.. Factors of Pisot tiling spaces and the coincidence rank conjecture. Bull. Soc. Math. France 143(2) (2015), 357–381.Google Scholar
Barge, M. and Diamond, B.. A complete invariant for the topology of one-dimensional substitution tiling spaces. Ergod. Th. & Dynam. Sys. 21 (2001), 1333–1358.Google Scholar
Barge, M. and Diamond, B.. Coincidence for substitutions of Pisot type. Bull. Soc. Math. France 130 (2002), 619–626.Google Scholar
Barge, M. and Gambaudo, J.-M.. Geometric realization for substitution tilings. Ergod. Th. & Dynam. Sys. 34(2) (2014), 457–482.CrossRefGoogle Scholar
Barge, M. and Kellendonk, J.. Proximality and pure point spectrum for tiling dynamical systems. Michigan Math. J. 62(4) (2013), 793–822.Google Scholar
Barge, M. and Kwapisz, J.. Geometric theory of unimodular Pisot substitutions. Amer. J. Math. 128 (2006), 1219–1282.Google Scholar
Barge, M. and Olimb, C.. Asymptotic structure in substitution tiling spaces. Ergod. Th. & Dynam. Sys. 34(1) (2014), 55–94.CrossRefGoogle Scholar
Barge, M., Štimac, S. and Williams, R. F.. Pure discrete spectrum in substitution tiling spaces. Discrete. Contin. Dyn. Syst. Ser. A 2 (2013), 579–597.Google Scholar
Berthé, V. and Siegel, A.. Tilings associated with beta-numeration and substitutions. Integers 5 (2005), A02.Google Scholar
Bertrand-Mathis, A.. Développements en base de Pisot et répartition modulo 1. C. R. Acad. Sci. Paris 285(6) (1977), A419–A421.Google Scholar
Blanchard, F.. 𝛽-expansion and symbolic dynamics. Theoret. Comput. Sci. 65 (1989), 131–141.Google Scholar
le Borgne, S.. Un codage sofique des automorphismes hyperboliques du tore. C. R. Acad. Sci. Paris 323 (1996), 1123–1128.Google Scholar
Clark, A. and Sadun, L.. When size matters: subshifts and their related tiling spaces. Ergod. Th. & Dynam. Sys. 23 (2003), 1043–1057.CrossRefGoogle Scholar
Ei, H. and Ito, S.. Tilings from some non-irreducible, Pisot substitutions. Discrete Math. Theor. Comput. Sci. 8(1) (2005), 81–122.Google Scholar
Dworkin, S.. Spectral theory and x-ray diffraction. J. Math. Phys. 34 (1993), 2964–2967.Google Scholar
Durand, F.. A characterization of substitutive sequences using return words. Discrete Math. 179 (1998), 89–101.Google Scholar
Frougny, C. and Solomyak, B.. Finite beta-expansions. Ergod. Th. & Dynam. Sys. 12 (1992), 713–723.Google Scholar
Hofbauer, F.. 𝛽-shifts have unique maximal measure. Monatsh. Math. 85 (1978), 189–198.Google Scholar
Hofbauer, F.. Maximal measures for simple piecewise monotonic transformations. Z. Wahrsch. Verw. Gebiete 52 (1980), 289–300.Google Scholar
Hollander, M.. Linear Numeration systems, finite beta expansions, and discrete spectrum of substitution dynamical systems. PhD Thesis, University of Washington, 1996.Google Scholar
Ito, S. and Takahashi, Y.. Markov subshifts and realization of 𝛽-expansions. J. Math Soc. Japan 26(1) (1974), 33–55.Google Scholar
Kalle, C. and Steiner, W.. Beta-expansions, natural extensions and multiple tilings associated with Pisot units. Trans. Amer. Math. Soc. 364(5) (2012), 2281–2318.Google Scholar
Kenyon, R. and Vershik, A.. Arithmetic construction of sofic partitions and hyperbolic toral automorphisms. Ergod. Th. & Dynam. Sys. 18 (1998), 357–372.Google Scholar
Lenz, D.. Aperiodic order and pure point diffraction. Philos. Mag. 88(13–15) (2008), 2059–2071.Google Scholar
D., Lind and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Lee, J.-Y., Moody, R. and Solomyak, B.. Consequences of pure point diffraction spectra for multiset substitution systems. Discrete Comput. Geom. 29 (2003), 525–560.Google Scholar
Lee, J.-Y. and Solomyak, B.. Pisot family self-affine tilings, discrete spectrum, and the Meyer property. Discrete Contin. Dyn. Syst. Ser. A 32(3) (2012), 935–959.Google Scholar
Parry, W.. On the 𝛽-expansions of real numbers. Acta Math. Hungar. 11 (1960), 269–278.Google Scholar
Praggastis, B.. Markov partition for hyperbolic toral automorphism. PhD Thesis, University of Washington, 1992.Google Scholar
Queffélec, M.. Substitution Dynamical Systems—Spectral Analysis (Lecture Notes in Mathematics, 1294) . Springer, Berlin, 1987.Google Scholar
Rauzy, G.. Nombres Algébriques et substitutions. Bull. Soc. Math. France 110 (1982), 147–178.Google Scholar
Rényi, A.. Representation for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hungary 8 (1957), 477–493.Google Scholar
Robinson, E. A. Jr. Symbolic dynamics and tilings of Rd. Symbolic Dynamics and its Applications (Proceedings of Symposia in Applied Mathematics, 60) . American Mathematical Society, Providence, RI, 2004, pp. 81–119.Google Scholar
Schmidt, K.. On periodic expansions of Pisot numbers and Salem numbers. Bull. Lond. Math. Soc. 12 (1980), 269–278.Google Scholar
Schmidt, K.. Algebraic codings of expansive group automorphisms and two-sided beta-shifts. Monatsh. Math. 129 (2000), 37–61.Google Scholar
Sidorov, N.. Bijective and general arithmetic codings for Pisot toral automorphisms. J. Dyn. Control Syst. 7(4) (2001), 447–472.Google Scholar
Sidorov, N.. Arithmetic dynamics. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310) . Cambridge University Press, Cambridge, 2003, pp. 145–189.Google Scholar
Solomyak, B.. Substitutions, adic transformations and beta-expansions. Contemp. Math. 135 (1992), 361–372.Google Scholar
Solomyak, B.. Dynamics of self-similar tilings. Ergod. Th. & Dynam. Sys. 17 (1997), 695–738.Google Scholar
Solomyak, B.. Nonperiodicity implies unique composition for self-similar translationally finite tilings. Discrete Comput. Geom. 20 (1998), 265–279.Google Scholar
Solomyak, B.. Eigenfunctions for substitution tiling systems. Adv. Stud. Pure Math. 49 (2007), 433–454.Google Scholar
Thurston, W. P.. Groups, Tilings and Finite State Automata (AMS Colloquium Lectures) . American Mathematical Society, Boulder, CO, 1989.Google Scholar
Veech, W. A.. The equicontinuous structure relation for minimal Abelian transformation groups. Amer. J. Math. 90 (1968), 723–732.Google Scholar
Vershik, A.. The fibadic expansion of real numbers and adic transformations. Preprint, Mittag-Leffler Institute, 1991/92.Google Scholar
Vershik, A.. Arithmetic isomorphism of the toral hyperbolic automorphisms and sofic systems. Funct. Anal. Appl. 26 (1992), 170–173.Google Scholar