Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T00:28:06.305Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic domains of quasiregular maps

Published online by Cambridge University Press:  14 March 2017

DANIEL A. NICKS Open the ORCID record for DANIEL A. NICKS [Opens in a new window]  and
DAVID J. SIXSMITH
DANIEL A. NICKS
Affiliation:
School of Mathematical Sciences, University of Nottingham, Nottingham NG7 2RD, UK email [email protected], [email protected]
DAVID J. SIXSMITH
Affiliation:
School of Mathematical Sciences, University of Nottingham, Nottingham NG7 2RD, UK email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the iteration of quasiregular maps of transcendental type from 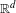$\mathbb{R}^{d}$ to 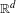$\mathbb{R}^{d}$. We give a bound on the rate at which the iterates of such a map can escape to infinity in a periodic component of the quasi-Fatou set. We give examples which show that this result is the best possible. Under an additional hypothesis, which is satisfied by all uniformly quasiregular maps, this bound can be improved to be the same as those in a Baker domain of a transcendental entire function. We construct a quasiregular map of transcendental type from 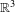$\mathbb{R}^{3}$ to 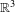$\mathbb{R}^{3}$ with a periodic domain in which all iterates tend locally uniformly to infinity. This is the first example of such behaviour in a dimension greater than two. Our construction uses a general result regarding the extension of bi-Lipschitz maps. In addition, we show that there is a quasiregular map of transcendental type from 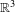$\mathbb{R}^{3}$ to 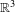$\mathbb{R}^{3}$ which is equal to the identity map in a half-space.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 6 , September 2018 , pp. 2321 - 2344
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, I. N.. Wandering domains in the iteration of entire functions. Proc. Lond. Math. Soc. (3) 49(3) (1984), 563–576.Google Scholar
Baker, I. N.. Infinite limits in the iteration of entire functions. Ergod. Th. & Dynam. Sys. 8(4) (1988), 503–507.Google Scholar
Barański, K. and Fagella, N.. Univalent Baker domains. Nonlinearity 14(3) (2001), 411–429.Google Scholar
Bergweiler, W.. Iteration of meromorphic functions. Bull. Amer. Math. Soc. (N.S.) 29(2) (1993), 151–188.Google Scholar
Bergweiler, W.. Singularities in Baker domains. Comput. Methods Funct. Theory 1(1) (2001), 41–49.Google Scholar
Bergweiler, W.. Fixed points of composite entire and quasiregular maps. Ann. Acad. Sci. Fenn. Math. 31(2) (2006), 523–540.Google Scholar
Bergweiler, W.. Karpińska’s paradox in dimension 3. Duke Math. J. 154(3) (2010), 599–630.Google Scholar
Bergweiler, W.. Fatou–Julia theory for non-uniformly quasiregular maps. Ergod. Th. & Dynam. Sys. 33(1) (2013), 1–23.Google Scholar
Bergweiler, W., Drasin, D. and Fletcher, A.. The fast escaping set for quasiregular mappings. Anal. Math. Phys. 4(1–2) (2014), 83–98.Google Scholar
Bergweiler, W. and Eremenko, A.. Dynamics of a higher dimensional analog of the trigonometric functions. Ann. Acad. Sci. Fenn. Math. 36(1) (2011), 165–175.Google Scholar
Bergweiler, W., Fletcher, A. and Nicks, D. A.. The Julia set and the fast escaping set of a quasiregular mapping. Comput. Methods Funct. Theory 14(2–3) (2014), 209–218.Google Scholar
Bergweiler, W. and Hinkkanen, A.. On semiconjugation of entire functions. Math. Proc. Cambridge Philos. Soc. 126(3) (1999), 565–574.Google Scholar
Bergweiler, W. and Nicks, D. A.. Foundations for an iteration theory of entire quasiregular maps. Israel J. Math. 201(1) (2014), 147–184.Google Scholar
Daneri, S. and Pratelli, A.. A planar bi-Lipschitz extension theorem. Adv. Calc. Var. 8(3) (2015), 221–266.Google Scholar
Evdoridou, V.. Fatou’s web. Proc. Amer. Math. Soc. 144 (2016), 5227–5524.Google Scholar
Fatou, P.. Sur l’itération des fonctions transcendantes entières. Acta Math. 47(4) (1926), 337–370.Google Scholar
Fletcher, A. N. and Nicks, D. A.. Chaotic dynamics of a quasiregular sine mapping. J. Difference Equ. Appl. 19(8) (2013), 1353–1360.Google Scholar
Fletcher, A. N. and Nicks, D. A.. Superattracting fixed points of quasiregular mappings. Ergod. Th. & Dynam. Sys. 36 (2016), 781–793.Google Scholar
García-Máynez, A. and Illanes, A.. A survey on unicoherence and related properties. An. Inst. Mat. Univ. Nac. Autónoma México 29 (1990), 17–67.Google Scholar
Herring, M. E.. Mapping properties of Fatou components. Ann. Acad. Sci. Fenn. Math. 23(2) (1998), 263–274.Google Scholar
Iwaniec, T. and Martin, G.. Quasiregular semigroups. Ann. Acad. Sci. Fenn. Math. 21(2) (1996), 241–254.Google Scholar
Iwaniec, T. and Martin, G.. Geometric Function Theory and Non-linear Analysis (Oxford Mathematical Monographs) . The Clarendon Press, Oxford University Press, New York, 2001.Google Scholar
Järvi, P.. On the zeros and growth of quasiregular mappings. J. Anal. Math. 82 (2000), 347–362.Google Scholar
Kalaj, D.. Radial extension of a bi-Lipschitz parametrization of a starlike Jordan curve. Complex Var. Elliptic Equ. 59(6) (2014), 809–825.Google Scholar
König, H.. Conformal conjugacies in Baker domains. J. Lond. Math. Soc. (2) 59(1) (1999), 153–170.Google Scholar
Kuratowski, K.. Topology Vol. II. New edition, revised and augmented. Translated from the French by A. Kirkor. Academic Press, New York; Państwowe Wydawnictwo Naukowe Polish Scientific Publishers, Warsaw, 1968.Google Scholar
Kuusalo, T.. Generalized conformal capacity and quasiconformal metrics. Proceedings of the Romanian–Finnish Seminar on Teichmüller Spaces and Quasiconformal Mappings (Braşov, 1969). Publishing House of the Academy of the Socialist Republic of Romania, Bucharest, 1971, pp. 193–202.Google Scholar
Mohri, M.. Quasiconformal metric and its application to quasiregular mappings. Osaka J. Math. 21(2) (1984), 225–237.Google Scholar
Nicks, D. A. and Sixsmith, D.. Hollow quasi-Fatou components of quasiregular maps. Math. Proc. Cambridge Philos. Soc. (2015), published online doi:10.1017/S0305004116000840.Google Scholar
Rickman, S.. Quasiregular Mappings (Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 26) . Springer, Berlin, 1993.Google Scholar
Rippon, P. J.. Baker domains of meromorphic functions. Ergod. Th. & Dynam. Sys. 26(4) (2006), 1225–1233.Google Scholar
Rippon, P. J.. Baker domains. Transcendental Dynamics and Complex Analysis (London Mathematical Society Lecture Note Series, 348) . Cambridge University Press, Cambridge, 2008, pp. 371–395.Google Scholar
Rippon, P. J. and Stallard, G. M.. On sets where iterates of a meromorphic function zip towards infinity. Bull. Lond. Math. Soc. 32(5) (2000), 528–536.Google Scholar
Rippon, P. J. and Stallard, G. M.. Fast escaping points of entire functions. Proc. Lond. Math. Soc. (3) 105(4) (2012), 787–820.Google Scholar
Rippon, P. J. and Stallard, G. M.. A sharp growth condition for a fast escaping spider’s web. Adv. Math. 244 (2013), 337–353.Google Scholar
Tukia, P.. The planar Schönflies theorem for Lipschitz maps. Ann. Acad. Sci. Fenn. Ser. A I Math. 5(1) (1980), 49–72.Google Scholar
Vuorinen, M.. Conformal Geometry and Quasiregular Mappings (Lecture Notes in Mathematics, 1319) . Springer, Berlin, 1988.Google Scholar
Zorich, V. A.. A theorem of M. A. Lavrent’ev on quasiconformal space maps. Mat. Sb. (N. S.) 74(116) (1967), 417–433.Google Scholar