Article contents
Periodic approximation of Lyapunov exponents for Banach cocycles
Published online by Cambridge University Press: 20 June 2017
Abstract
We consider group-valued cocycles over dynamical systems. The base system is a homeomorphism 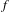 $f$ of a metric space satisfying a closing property, for example a hyperbolic dynamical system or a subshift of finite type. The cocycle
$f$ of a metric space satisfying a closing property, for example a hyperbolic dynamical system or a subshift of finite type. The cocycle 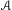 $A$ takes values in the group of invertible bounded linear operators on a Banach space and is Hölder continuous. We prove that upper and lower Lyapunov exponents of
$A$ takes values in the group of invertible bounded linear operators on a Banach space and is Hölder continuous. We prove that upper and lower Lyapunov exponents of 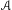 $A$ with respect to an ergodic invariant measure
$A$ with respect to an ergodic invariant measure  $\unicode[STIX]{x1D707}$ can be approximated in terms of the norms of the values of
$\unicode[STIX]{x1D707}$ can be approximated in terms of the norms of the values of 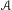 $A$ on periodic orbits of
$A$ on periodic orbits of 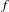 $f$. We also show that these exponents cannot always be approximated by the exponents of
$f$. We also show that these exponents cannot always be approximated by the exponents of 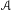 $A$ with respect to measures on periodic orbits. Our arguments include a result of independent interest on construction and properties of a Lyapunov norm for the infinite-dimensional setting. As a corollary, we obtain estimates of the growth of the norm and of the quasiconformal distortion of the cocycle in terms of the growth at the periodic points of
$A$ with respect to measures on periodic orbits. Our arguments include a result of independent interest on construction and properties of a Lyapunov norm for the infinite-dimensional setting. As a corollary, we obtain estimates of the growth of the norm and of the quasiconformal distortion of the cocycle in terms of the growth at the periodic points of 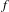 $f$.
$f$.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 5
- Cited by


