Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T05:04:50.521Z Has data issue: false hasContentIssue false
  • English
  • Français

Orbits of homogeneous polynomials on Banach spaces

Part of: Nonlinear operators and their properties Complex dynamical systems Holomorphic mappings and correspondences General theory of linear operators

Published online by Cambridge University Press:  13 April 2020

RODRIGO CARDECCIA  and
SANTIAGO MURO
RODRIGO CARDECCIA
Affiliation:
Departamento de Matemática – PAB I, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, (1428) Buenos Aires, Argentina email [email protected] IMAS-CONICET, Universidad de Buenos Aires, (1428) Buenos Aires, Argentina
SANTIAGO MURO
Affiliation:
Facultad de Ciencias Exactas, Ingenieria y Agrimensura, Universidad Nacional de Rosario, Argentina CIFASIS-CONICET, Universidad Nacional de Rosario, Argentina email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the dynamics induced by homogeneous polynomials on Banach spaces. It is known that no homogeneous polynomial defined on a Banach space can have a dense orbit. We show a simple and natural example of a homogeneous polynomial with an orbit that is at the same time $\unicode[STIX]{x1D6FF}$-dense (the orbit meets every ball of radius $\unicode[STIX]{x1D6FF}$), weakly dense and such that 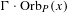$\unicode[STIX]{x1D6E4}\cdot \text{Orb}_{P}(x)$ is dense for every 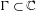$\unicode[STIX]{x1D6E4}\subset \mathbb{C}$ that either is unbounded or has 0 as an accumulation point. Moreover, we generalize the construction to arbitrary infinite-dimensional separable Banach spaces. To prove this, we study Julia sets of homogeneous polynomials on Banach spaces.

Keywords

Polynomical dynamicshypercyclic operatorsJulia sets

MSC classification

Primary: 47H60: Multilinear and polynomial operators 37F10: Polynomials; rational maps; entire and meromorphic functions
Secondary: 47A16: Cyclic vectors, hypercyclic and chaotic operators 32H50: Iteration problems
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 6 , June 2021 , pp. 1627 - 1655
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ansari, S. I.. Existence of hypercyclic operators on topological vector spaces. J. Funct. Anal. 148(2) (1997), 384–390.CrossRefGoogle Scholar
Appell, J., De Pascale, E. and Vignoli, A.. Nonlinear Spectral Theory, Vol. 10. Walter de Gruyter, Berlin, 2004.CrossRefGoogle Scholar
Aron, R. M. and Miralles, A.. Chaotic polynomials in spaces of continuous and differentiable functions. Glasg. Math. J. 50(2) (2008), 319–323.CrossRefGoogle Scholar
Bayart, F. and Matheron, E.. Dynamics of Linear Operators (Cambridge Tracts in Mathematics, 179) . Cambridge University Press, Cambridge, 2009, p. xiv, 337 p.CrossRefGoogle Scholar
Beauzamy, B.. Introduction to Operator Theory and Invariant Subspaces, Vol. 42. North-Holland, Amsterdam, 1988.Google Scholar
Bermúdez, T., Bonilla, A., Martínez-Giménez, F. and Peris, A.. Li–Yorke and distributionally chaotic operators. J. Math. Anal. Appl. 373(1) (2011), 83–93.CrossRefGoogle Scholar
Bermúdez, T., Bonilla, A. and Peris, A.. ℂ-supercyclic versus ℝ+ -supercyclic operators. Arch. Math. 79(2) (2002), 125–130.Google Scholar
Bernal-González, L.. On hypercyclic operators on Banach spaces. Proc. Amer. Math. Soc. 127(4) (1999), 1003–1010.CrossRefGoogle Scholar
Bernardes, N., Bonilla, A., Müller, V. and Peris, A.. Li–Yorke chaos in linear dynamics. Ergod. Theory Dyn. Sys. 35(6) (2015), 1723–1745.CrossRefGoogle Scholar
Bernardes, N. C.. On orbits of polynomial maps in Banach spaces. Quaest. Math. 21(3–4) (1998), 311–318.CrossRefGoogle Scholar
Bernardes, N. C., Bonilla, A., Müller, V. and Peris, A.. Distributional chaos for linear operators. J. Funct. Anal. 265(9) (2013), 2143–2163.CrossRefGoogle Scholar
Bernardes, N. C. and Peris, A.. On the existence of polynomials with chaotic behaviour. J. Funct. Spaces Appl. 2013 (2013), 320961.CrossRefGoogle Scholar
Bès, J. and Conejero, J. A.. An extension of hypercyclicity for N-linear operators. Abstr. Appl. Anal. 2014 (2014), 609873.CrossRefGoogle Scholar
Bonet, J. and Peris, A.. Hypercyclic operators on non-normable Fréchet spaces. J. Funct. Anal. 159(2) (1998), 587–595.CrossRefGoogle Scholar
Bourdon, P. S. and Feldman, N. S.. Somewhere dense orbits are everywhere dense. Indiana Univ. Math. J. 52(3) (2003), 811–819.CrossRefGoogle Scholar
Cardeccia, R.. Hypercyclic bilinear operators on Banach spaces. J. Math. Anal. Appl. 485(1) (2020),123771.CrossRefGoogle Scholar
Cardeccia, R. and Muro, S.. Hypercyclic homogeneous polynomials on H (ℂ). J. Approx. Theory 226 (2018), 60–72.CrossRefGoogle Scholar
Chan, K. C. and Sanders, R.. A weakly hypercyclic operator that is not norm hypercyclic. J. Oper. Theory 52(1) (2004), 39–59.Google Scholar
Charpentier, S., Ernst, R. and Menet, Q.. 𝛤-supercyclicity. J. Funct. Anal. 270(12) (2016), 4443–4465.CrossRefGoogle Scholar
Dinh, T.-C. and Sibony, N.. Dynamics in several complex variables: endomorphisms of projective spaces and polynomial-like mappings. Holomorphic Dynamical Systems (Lecture Notes in Mathematics, 1998) . Eds. Gentili, G., Guenot, J. and Patrizio, G.. Springer, Heidelberg, 2010, pp. 165–294.CrossRefGoogle Scholar
Feldman, N. S.. Perturbations of hypercyclic vectors. J. Math. Anal. Appl. 273(1) (2002), 67–74.CrossRefGoogle Scholar
Grosse-Erdmann, K.-G. and Kim, S. G.. Bihypercyclic bilinear mappings. J. Math. Anal. Appl. 399(2) (2013), 701–708.CrossRefGoogle Scholar
Grosse-Erdmann, K.-G. and Peris Manguillot, A.. Linear Chaos. Springer, London, 2011.CrossRefGoogle Scholar
Hájek, P., Montesinos Santalucía, V., Vanderwerff, J. and Zizler, V.. Biorthogonal Systems in Banach Spaces. Springer, New York, 2008.Google Scholar
Kim, S. G., Peris, A. and Song, H. G.. Numerically hypercyclic operators. Integral Equations Operator Theory 72(3) (2012), 393–402.CrossRefGoogle Scholar
Kim, S. G., Peris, A. and Song, H. G.. Numerically hypercyclic polynomials. Arch. Math. 99(5) (2012), 443–452.CrossRefGoogle Scholar
León-Saavedra, F. and Müller, V.. Rotations of hypercyclic and supercyclic operators. Integral Equations Operator Theory 50(3) (2004), 385–391.CrossRefGoogle Scholar
Martínez-Giménez, F. and Peris, A.. Existence of hypercyclic polynomials on complex Fréchet spaces. Topol. Appl. 156(18) (2009), 3007–3010.CrossRefGoogle Scholar
Martínez-Giménez, F. and Peris, A.. Chaotic polynomials on sequence and function spaces. Intl J. Bifurcation Chaos 20(09) (2010), 2861–2867.CrossRefGoogle Scholar
Peris, A.. Erratum to: ‘Chaotic polynomials on Fréchet spaces’. Proc. Amer. Math. Soc. 129(12) (2001), 3759–3760.CrossRefGoogle Scholar
Peris, A.. Chaotic polynomials on Banach spaces. J. Math. Anal. Appl. 287(2) (2003), 487–493.CrossRefGoogle Scholar
León Saavedra, F.. The positive supercyclicity theorem. Extracta Math. 19(1) (2004), 145–149.Google Scholar
Schweizer, B. and Smital, J.. Measures of chaos and a spectral decomposition of dynamical systems on the interval. Trans. Amer. Math. Soc. 344(2) (1994), 737–754.CrossRefGoogle Scholar
Ueda, T.. Fatou sets in complex dynamics on projective spaces. J. Math. Soc. Japan 46(3) (1994), 545–555.CrossRefGoogle Scholar