Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:38:42.559Z Has data issue: false hasContentIssue false
  • English
  • Français

One-sided almost specification and intrinsic ergodicity

Published online by Cambridge University Press:  18 January 2018

VAUGHN CLIMENHAGA  and
RONNIE PAVLOV
VAUGHN CLIMENHAGA
Affiliation:
Department of Mathematics, University of Houston, 4800 Calhoun St., Houston, TX 77204, USA email [email protected]
RONNIE PAVLOV
Affiliation:
Department of Mathematics, University of Denver, 2290 S. York St., Denver, CO 80208, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We define a new property called one-sided almost specification, which lies between the properties of specification and almost specification, and prove that it guarantees intrinsic ergodicity (i.e. uniqueness of the measure of maximal entropy) if the corresponding mistake function $g$ is bounded. We also show that uniqueness may fail for unbounded $g$ such as 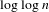$\log \log n$. Our results have consequences for almost specification: we prove that almost specification with 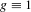$g\equiv 1$ implies one-sided almost specification (with 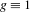$g\equiv 1$) and hence uniqueness. On the other hand, the second author showed recently that almost specification with 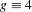$g\equiv 4$ does not imply uniqueness.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 9 , September 2019 , pp. 2456 - 2480
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertrand, A.. Specification, synchronisation, average length. Coding Theory and Applications (Cachan, 1986) (Lecture Notes in Computer Science, 311) . Springer, Berlin, 1988, pp. 86–95.Google Scholar
Bowen, R.. Periodic points and measures for Axiom A diffeomorphisms. Trans. Amer. Math. Soc. 154 (1971), 377–397.Google Scholar
Bowen, R.. Some systems with unique equilibrium states. Math. Systems Theory 8(3) (1974–1975), 193–202.Google Scholar
Buzzi, J.. Specification on the interval. Trans. Amer. Math. Soc. 349(7) (1997), 2737–2754.Google Scholar
Climenhaga, V.. Specification and towers in shift spaces. Preprint, 2015, arXiv:1502.00931v2, submitted.Google Scholar
Climenhaga, V. and Thompson, D. J.. Intrinsic ergodicity beyond specification: 𝛽-shifts, S-gap shifts, and their factors. Israel J. Math. 192(2) (2012), 785–817.Google Scholar
Coven, E. M. and Smítal, J.. Entropy-minimality. Acta Math. Univ. Comenian. (N.S.) 62(1) (1993), 117–121.Google Scholar
Kulczycki, M., Kwietniak, D. and Oprocha, P.. On almost specification and average shadowing properties. Fund. Math. 224(3) (2014), 241–278.Google Scholar
Kwietniak, D., Oprocha, P. and Rams, M.. On entropy of dynamical systems with almost specification. Israel J. Math. 213(1) (2016), 475–503.Google Scholar
Parry, W.. Intrinsic Markov chains. Trans. Amer. Math. Soc. 112 (1964), 55–66.Google Scholar
Pavlov, R.. On intrinsic ergodicity and weakenings of the specification property. Adv. Math. 295 (2016), 250–270.Google Scholar
Pavlov, R.. On non-uniform specification and uniqueness of the equilibrium state in expansive systems. Preprint, 2017, arXiv:1702.02870v3, submitted.Google Scholar
Pfister, C.-E. and Sullivan, W. G.. Large deviations estimates for dynamical systems without the specification property. Applications to the 𝛽-shifts. Nonlinearity 18(1) (2005), 237–261.Google Scholar
Pfister, C.-E. and Sullivan, W. G.. On the topological entropy of saturated sets. Ergod. Th. & Dynam. Sys. 27(3) (2007), 929–956.Google Scholar
Quas, A. N. and Trow, P. B.. Subshifts of multi-dimensional shifts of finite type. Ergod. Th. & Dynam. Sys. 20(3) (2000), 859–874.Google Scholar
Schmeling, J.. Symbolic dynamics for 𝛽-shifts and self-normal numbers. Ergod. Th. & Dynam. Sys. 17(3) (1997), 675–694.Google Scholar
Stanley, B.. Bounded density shifts. Ergod. Th. & Dynam. Sys. 33(6) (2013), 1891–1928.Google Scholar
Thompson, D. J.. Irregular sets, the 𝛽-transformation and the almost specification property. Trans. Amer. Math. Soc. 364(10) (2012), 5395–5414.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar
Weiss, B.. Intrinsically ergodic systems. Bull. Amer. Math. Soc. 76 (1970), 1266–1269.Google Scholar
Wu, X., Oprocha, P. and Chen, G.. On various definitions of shadowing with average error in tracing. Nonlinearity 29(7) (2016), 1942–1972.Google Scholar