Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:38:22.739Z Has data issue: false hasContentIssue false
  • English
  • Français

On the transfer operator for rational functions on the Riemann sphere

Published online by Cambridge University Press:  19 September 2008

Manfred Denker ,
Feliks Przytycki  and
Mariusz Urbański
Manfred Denker
Affiliation:
Institut für Mathematische Stochastik, Universität Göttingen, Lotzestraβe 13, 37083 Göttingen, Germany
Feliks Przytycki
Affiliation:
Institute of Mathematics, Polish Academy of Science, ul. Śniadeckich 8, 00-950 Warsaw, Poland
Mariusz Urbański
Affiliation:
Institute of Mathematics, Polish Academy of Science, ul. Śniadeckich 8, 00-950 Warsaw, Poland Department of Mathematics, University of North Texas, Denton TX 76203-5116, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

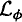Let T be a rational function of degree ≥ 2 on the Riemann sphere. Our results are based on the lemma that the diameter of a connected component of T−n(B(x, r)), centered at any point x in its Julia set J = J(T), does not exceed Lnrp for some constants L ≥ 1 and ρ > 0. Denote the transfer operator of a Hölder-continuous function φ on J satisfying P(T,φ) > supz∈Jφ(z). We study the behavior of {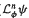: n ≥ 1} for Hölder-continuous functions ψ and show that the sequence is (uniformly) normbounded in the space of Hölder-continuous functions for sufficiently small exponent. As a consequence we obtain that the density of the equilibrium measure μ for φ with respect to the 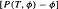-conformal measure is Höolder-continuous. We also prove that the rate of convergence of {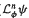ψ to this density in sup-norm is 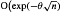. From this we deduce the corresponding decay of the correlation integral and the central limit theorem for ψ.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 16 , Issue 2 , April 1996 , pp. 255 - 266
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bowen, R.. Equilibrium states and the ergodic theory of Anosov diffeomorphsms. Springer Lecture Notes in Mathematics 470. Springer, Berlin, 1975.Google Scholar
[2]Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic theory on compact spaces. Springer Lecture Notes in Mathematics 527. Springer, Berlin, 1976.Google Scholar
[3]Denker, M. and Urbański, M.. Ergodic theory of equilibrium states for rational maps. Nonlinearity 4 (1991), 103–134.CrossRefGoogle Scholar
[4]Denker, M. and Urbański, M.. The dichotomy of Hausdorff measures and equilibrium states for parabolic rational maps. Ergodic Theory and Related Topics III, Proceedings Güstrow 1990, eds. Krengel, U., Richter, K. and Warstat, V.. Lecture Notes in Mathematics 1514. Springer, Berlin, 1992, pp. 90–113.Google Scholar
[5]Gordin, M. I.. The central limit theorem for stationary processes. Dokl. Akad. Nauk SSSR 188 (1969), 739–741. Engl. Transl.: Sov. Math. Dokl. 10, (1969), 1174–1176.Google Scholar
[6]Hofbauer, F. and Keller, G.. Equilibrium states for piecewise monotonic maps. Ergod. Th. & Dynam. Sys. 2 (1982), 23–43.CrossRefGoogle Scholar
[7]Keller, G.. Un théorème de la limite centrale pour une classe de transformations monotones par morceaux. C.R. Acad. Sc. Paris 291 (1980), 155–158.Google Scholar
[8]Przytycki, F.. On the Perron—Frobenius-Ruelle operator for rational maps on the Riemann sphere and for Hölder continuous functions. Bol. Soc. Bras. Mat. 20 (1990), 95–125.CrossRefGoogle Scholar
[9]Przytycki, F.. Lyapunov characteristic exponents are non-negative. Proc. Amer. Math. Soc. 119 (1993), 309–317.Google Scholar
[10]Ruelle, D.. Thermodynamic Formalism. Encyclopedia in Math, and its Appl. Vol. 5. Addison-Wesley, 1978.Google Scholar
[11]Ziemian, K.. Almost sure invariance principles for some maps of the interval. Ergod. Th. & Dynam. Sys. 5 (1985), 625–640.CrossRefGoogle Scholar