Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-17T00:16:51.878Z Has data issue: false hasContentIssue false
  • English
  • Français

On the specification property and synchronization of unique q-expansions

Part of: Elementary number theory Topological dynamics Discrete mathematics in relation to computer science

Published online by Cambridge University Press:  28 September 2020

RAFAEL ALCARAZ BARRERA
RAFAEL ALCARAZ BARRERA*
Affiliation:
Instituto de Física, Universidad Autónoma de San Luis Potosí, Av. Manuel Nava 6, Zona Universitaria, C.P. 78290. San Luis Potosí, S.L.P. México (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

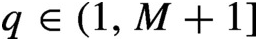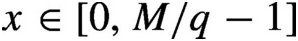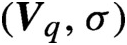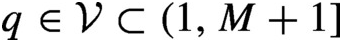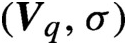Given a positive integer M and $q \in (1, M+1]$ we consider expansions in base q for real numbers $x \in [0, {M}/{q-1}]$ over the alphabet $\{0, \ldots , M\}$ . In particular, we study some dynamical properties of the natural occurring subshift $(\boldsymbol{{V}}_q, \sigma )$ related to unique expansions in such base q. 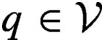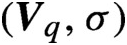We characterize the set of $q \in \mathcal {V} \subset (1,M+1]$ such that $(\boldsymbol{{V}}_q, \sigma )$ has the specification property and the set of $q \in \mathcal {V}$ such that $(\boldsymbol{{V}}_q, \sigma )$ is a synchronized subshift. Such properties are studied by analysing the combinatorial and dynamical properties of the quasi-greedy expansion of q. We also calculate the size of such classes as subsets of 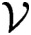$\mathcal {V}$ giving similar results to those shown by Blanchard [ 10 ] and Schmeling in [ 36 ] in the context of 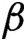$\beta $ -transformations.

Keywords

expansions in non integer basesspecification propertysynchronized systemsHausdorff dimension

MSC classification

Primary: 37B10: Symbolic dynamics 11A63: Radix representation; digital problems
Secondary: 37B40: Topological entropy 68R15: Combinatorics on words
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 9 , September 2021 , pp. 2659 - 2705
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alcaraz Barrera, R.. Topological and ergodic properties of symmetric sub-shifts. Discrete Contin. Dyn. Syst. 34(11) (2014), 4459–4486.CrossRefGoogle Scholar
Alcaraz Barrera, R., Baker, S. and Kong, D.. Entropy, topological transitivity, and dimensional properties of unique $q$ -expansions. Trans. Amer. Math. Soc. 371(5) (2019), 3209–3258.CrossRefGoogle Scholar
Allaart, P. and Kong, D.. On the continuity of the Hausdorff dimension of the univoque set. Adv. Math. 354 (2019), 106729.CrossRefGoogle Scholar
Allaart, P. C.. On univoque and strongly univoque sets. Adv. Math. 308 (2017), 575–598.CrossRefGoogle Scholar
Allouche, J., Clarke, M. and Sidorov, N.. Periodic unique beta-expansions: the Sharkovskǐ ordering. Ergod. Th. & Dynam. Sys. 29(4) (2009), 1055–1074.CrossRefGoogle Scholar
Baiocchi, C. and Komornik, V.. Greedy and quasi-greedy expansions in non-integer bases. Preprint, 2007, https://arxiv.org/pdf/0710.3001.pdf.Google Scholar
Baker, S.. Generalized golden ratios over integer alphabets. Integers 14 (2014), paper a15, 28.Google Scholar
Baker, S. and Ghenciu, A. E.. Dynamical properties of $S$ -gap shifts and other shift spaces. J. Math. Anal. Appl. 430(2) (2015), 633–647.CrossRefGoogle Scholar
Bertrand-Mathis, A.. Développement en base $\theta$ ; répartition modulo un de la suite ${(x{\theta}^n)}_{n\ge 0}$ ; langages codés et $\theta$ -shift. Bull. Soc. Math. France 114(3) (1986), 271–323.CrossRefGoogle Scholar
Blanchard, F.. $\beta$ -expansions and symbolic dynamics. Theoret. Comput. Sci. 65(2) (1989), 131–141.CrossRefGoogle Scholar
Boyle, M.. Algebraic aspects of symbolic dynamics. Topics in Symbolic Dynamics and Applications (Temuco, 1997) (London Mathematical Society Lecture Note Series, 279). Cambridge University Press, Cambridge, 2000, pp. 57–88.Google Scholar
Allaart, P. C.. An algebraic approach to entropy plateaus in non-integer base expansions. Discrete Contin. Dyn. Syst. 39(11) (2019), 6507–6522.CrossRefGoogle Scholar
Daróczy, Z. and Kátai, I.. On the structure of univoque numbers. Publ. Math. Debrecen 46(3–4) (1995), 385–408.Google Scholar
de Vries, M. and Komornik, V.. Unique expansions of real numbers. Adv. Math. 221(2) (2009), 390–427.CrossRefGoogle Scholar
de Vries, M., Komornik, V. and Loreti, P.. Topology of the set of univoque bases. Topology Appl. 205 (2016), 117–137. The Pisot Substitution Conjecture.CrossRefGoogle Scholar
Erdős, P. and Joó, I.. On the number of expansions $1=\sum {q}^{-{n}_i}$ . Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 35 (1992), 129–132.Google Scholar
Erdős, P., Joó, I. and Komornik, V.. Characterization of the unique expansions $1={\sum}_{i=1}^{\infty }{q}^{-{n}_i}$ and related problems. Bull. Soc. Math. France 118(3) (1990), 377–390.CrossRefGoogle Scholar
Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications. John Wiley, Chichester, 1990.Google Scholar
Faller, B. and Pfister, C.-E.. A point is normal for almost all maps $\beta\mathrm{x}+\alpha mod1$ or generalized $\beta$ -transformations. Ergod. Th. & Dynam. Sys. 29(5) (2009), 1529–1547.CrossRefGoogle Scholar
Fiebig, D. and Fiebig, U.. Invariants for subshifts via nested sequences of shifts of finite type. Ergod. Th. & Dynam. Sys. 21(6) (2001), 1731–1758.CrossRefGoogle Scholar
García-Ramos, F. and Pavlov, R.. Extender sets and measures of maximal entropy for subshifts. J. Lond. Math. Soc. (2) 100(3) (2019), 1013–1033.CrossRefGoogle Scholar
Ge, Y. and Tan, B.. Periodicity of the univoque $\beta$ -expansions. Acta Math. Sci. Ser. B (Engl. Ed.) 37(1) (2017), 33–46.Google Scholar
Kalle, C., Kong, D., Li, W. and Lü, F.. On the bifurcation set of unique expansions. Acta Arith. 188(4) (2019), 367–399.CrossRefGoogle Scholar
Kalle, C. and Steiner, W.. Beta-expansions, natural extensions and multiple tilings associated with Pisot units. Trans. Amer. Math. Soc. 364(5) (2012), 2281–2318.CrossRefGoogle Scholar
Komornik, V.. Expansions in noninteger bases. Integers 11B (2011), paper a9, 30.Google Scholar
Komornik, V., Kong, D. and Li, W.. Hausdorff dimension of univoque sets and devil’s staircase. Adv. Math. 305 (2017), 165–196.CrossRefGoogle Scholar
Komornik, V. and Loreti, P.. Subexpansions, superexpansions and uniqueness properties in non-integer bases. Period. Math. Hungar. 44(2) (2002), 197–218.CrossRefGoogle Scholar
Komornik, V. and Loreti, P.. On the topological structure of univoque sets. J. Number Theory 122(1) (2007), 157–183.CrossRefGoogle Scholar
Kong, D. and Li, W.. Hausdorff dimension of unique beta expansions. Nonlinearity 28(1) (2015), 187–209.CrossRefGoogle Scholar
Krieger, W.. On Subshifts and Topological Markov Chains. Springer US, Boston, MA, 2000, pp. 453–472.Google Scholar
Kwietniak, D., Ła̧cka, M. and Oprocha, P.. A panorama of specification-like properties and their consequences. Dynamics and Numbers (Contemporary Mathematics, 669). American Mathematical Society, Providence, RI, 2016, pp. 155–186.CrossRefGoogle Scholar
Li, B., Sahlsten, T. and Samuel, T.. Intermediate $\beta$ -shifts of finite type. Discrete Contin. Dyn. Syst. 36(1) (2016), 323–344.CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Parry, W.. On the $\beta$ -expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.CrossRefGoogle Scholar
Rényi, A.. Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hungar. 8 (1957), 477–493.CrossRefGoogle Scholar
Schmeling, J.. Symbolic dynamics for $\beta$ -shifts and self-normal numbers. Ergod. Th. & Dynam. Sys. 17 6 (1997), 675–694.CrossRefGoogle Scholar
Sidorov, N.. Almost every number has a continuum of $\beta$ -expansions. Amer. Math. Monthly 110(9) (2003), 838–842.Google Scholar
Sidorov, N.. Arithmetic dynamics. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310). Cambridge University Press, Cambridge, 2003, pp. 145–189.CrossRefGoogle Scholar
Sidorov, N.. Expansions in non-integer bases: lower, middle and top orders. J. Number Theory 129(4) (2009), 741–754.CrossRefGoogle Scholar
Urbański, M.. Invariant subsets of expanding mappings of the circle Ergod. Th. & Dynam. Sys. 7(4) (1987), 627–645.CrossRefGoogle Scholar