Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T14:53:37.076Z Has data issue: false hasContentIssue false
  • English
  • Français

On the rigidity of quasiconformal Anosov flows

Published online by Cambridge University Press:  01 December 2007

YONG FANG
YONG FANG*
Affiliation:
Département de Mathématiques, Université de Cergy-Pontoise, avenue Adolphe Chauvin, 95302 Cergy-Pontoise Cedex, France (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop further our study of quasiconformal Anosov flows in our previous (Y. Fang. Smooth rigidity of uniformly quasiconformal Anosov flows. Ergod. Th. & Dynam. Sys.24 (2004), 1–23). For example, we prove the following result: Let φ be a transversely symplectic Anosov flow with dim  Ess≥2 and dim  Esu≥2. If φ is quasiconformal, then it is, up to finite covers, 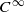orbit equivalent either to the suspension of a symplectic hyperbolic automorphism of a torus or to the geodesic flow of a closed hyperbolic manifold.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 27 , Issue 6 , December 2007 , pp. 1773 - 1802
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Anosov, V. D.. Geodesic flows on closed Riemannian manifolds with negative curvature. Proc. Inst. Steklov 90 (1967), 1–235.Google Scholar
[2]Brunella, M.. On transversely holomorphic flows I. Invent. Math. 126 (1996), 265–279.Google Scholar
[3]Barbot, T.. Caractérisation des flots d’Anosov en dimension 3 par leurs feuilletages faibles. Ergod. Th. & Dynam. Sys. 15 (1995), 247–270.Google Scholar
[4]Dumitrescu, S.. Métriques riemanniennes holomorphes en petite dimension. Ann. Inst. Fourier 51(6) (2001), 1663–1690.Google Scholar
[5]Fang, Y.. Smooth rigidity of uniformly quasiconformal Anosov flows. Ergod. Th. & Dynam. Sys. 24 (2004), 1–23.CrossRefGoogle Scholar
[6]Fang, Y.. Structures géométriques rigides et systèmes dynamiques hyperboliques. PhD Thesis, Université de Paris-Sud. Available at:http://tel.ccsd.cnrs.fr/documents/archives0/00/00/87/34/indexfr.html.Google Scholar
[7]Fang, Y.. A remark about hyperbolic infranilautomorphisms. C. R. Acad. Sci. Paris, Ser. I 336(9) (2003), 769–772.CrossRefGoogle Scholar
[8]Feres, R. and Katok, A.. Invariant tensor fields of dynamical systems with pinched Lyapunov exponents and rigidity of geodesic flows. Ergod. Th. & Dynam. Sys. 9 (1989), 427–432.CrossRefGoogle Scholar
[9]Ghys, É.. On transversely holomorphic flows II. Invent. Math. 126 (1996), 281–286.CrossRefGoogle Scholar
[10]Ghys, É.. Déformation des flots d’Anosov et de groupes fuchsiens. Ann. Inst. Fourier 42 (1992), 209–247.CrossRefGoogle Scholar
[11]Ghys, É.. Holomorphic Anosov flows. Invent. Math. 119 (1995), 585–614.Google Scholar
[12]Godbillon, C.. Feuilletages. Progr. Math. 98 (1991).Google Scholar
[13]Haefliger, A.. Groupoides d’holonomie et classifiants. Astérisque 116 (1984), 70–97.Google Scholar
[14]Hamenstädt, U.. Cocycles, symplectic structures and intersection. Geom. Funct. Anal. 9(1) (1999), 90–140.CrossRefGoogle Scholar
[15]Hamenstädt, U.. Invariant two-forms for geodesic flows. Math. Ann. 301(4) (1995), 677–698.CrossRefGoogle Scholar
[16]Kanai, M.. Differential-geometric studies on dynamics of geodesic and frame flows. Japan. J. Math. 19 (1993), 1–30.CrossRefGoogle Scholar
[17]Katok, A. and Hasselblatt, B.. Introduction to the modern theory of dynamical systems, vol. 54 (Encyclopedia of Mathematics and its Applications). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
[18]Katok, A. and Lewis, J.. Local rigidity for certain groups of toral automorphisms. Israel J. Math. 75 (1991), 203–241.CrossRefGoogle Scholar
[19]Kobayashi, S. and Nomisu, K.. Foundations of Differential Geometry. Vol. 2. Interscience, New York, 1963.Google Scholar
[20]Kalinin, B. and Sadovskaya, V.. On local and global rigidity of quasiconformal Anosov diffeomorphisms. J. Inst. Math. Jussieu 2(4) (2003), 567–582.CrossRefGoogle Scholar
[21]Livsic, A. N.. Cohomology of dynamical systems. Math. USSR Izvestija 6(6) (1972), 1278–1301.Google Scholar
[22]de La Llave, R.. Rigidity of higher-dimensional conformal Anosov systems. Ergod. Th. & Dynam. Sys. 22(6) (2002), 1845–1870.Google Scholar
[23]de La Llave, R.. Further rigidity properties of conformal Anosov systems. Ergod. Th.& Dynam. Sys. 24(5) (2004), 1425–1441.CrossRefGoogle Scholar
[24]de La Llave, R.. Smooth conjugacy and S-R-B measures for uniformly and non-uniformly hyperbolic systems. Comm. Math. Phys. 150 (1992), 289–320.CrossRefGoogle Scholar
[25]de La Llave, R. and Moriyón, R.. Invariants for smooth conjugacy of hyperbolic dynamical systems, IV. Comm. Math. Phys. 116(2) (1988), 185–192.Google Scholar
[26]de la Llave, R., Marco, J. and Moriyon, R.. Canonical perturbation theory of Anosov systems and regularity results for Livsic cohomology equation. Ann. of Math. 123(3) (1986), 537–612.Google Scholar
[27]Margulis, G. A.. The isometry of closed manifolds of constant negative curvature with the same fundamental group. Soviet Math. Dokl. 11 (1970), 722–723.Google Scholar
[28]McCleary, J.. User’s Guide to Spectral Sequences (Mathematics Lectures Series, 12). Publish or Perish, Wilmington, DE, 1985.Google Scholar
[29]Mostow, G. D.. Quasi-conformal mappings in n-space and the rigidity of hyperbolic space forms. Publ. Math. Inst. Hautes Études Sci. 34 (1968), 53–104.Google Scholar
[30]Paternain, G. P.. On the regularity of the Anosov splitting for twisted geodesic flows. Math. Res. Lett. 4 (1997), 871–888.CrossRefGoogle Scholar
[31]Paternain, G. P.. Geodesic flows. Progr. Math. 180 (1999).Google Scholar
[32]Plante, J. F.. Anosov flows. Amer. J. Math. 94 (1972), 729–754.CrossRefGoogle Scholar
[33]Plante, J.. Anosov flows, transversely affine foliations and a conjecture of Verjovsky. J. London Math. Soc. (2) 23 (1981), 359–362.Google Scholar
[34]Sadovskaya, V.. On uniformly quasiconformal Anosov systems. Math. Res. Lett. 12 (2005), 425–441.CrossRefGoogle Scholar
[35]Yue, C.. Quasiconformality in the geodesic flow of negatively curved manifolds. Geom. Funct. Anal. 6(4) (1996), 740–750.CrossRefGoogle Scholar