Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-17T15:23:14.686Z Has data issue: false hasContentIssue false
  • English
  • Français

On the random dynamics of Volterra quadratic operators

Published online by Cambridge University Press:  21 July 2015

U. U. JAMILOV ,
M. SCHEUTZOW  and
M. WILKE-BERENGUER
U. U. JAMILOV
Affiliation:
Institute of Mathematics, National University of Uzbekistan, 29, Do’rmon Yo’li str., 100125 Tashkent, Uzbekistan email [email protected]
M. SCHEUTZOW
Affiliation:
Institut für Mathematik, MA 7-5, Fakultät II, Technische Universität Berlin, Straße des 17. Juni 136, 10623 Berlin, Germany email [email protected], [email protected]
M. WILKE-BERENGUER
Affiliation:
Institut für Mathematik, MA 7-5, Fakultät II, Technische Universität Berlin, Straße des 17. Juni 136, 10623 Berlin, Germany email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

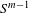We consider random dynamical systems generated by a special class of Volterra quadratic stochastic operators on the simplex $S^{m-1}$ . We prove that in contrast to the deterministic set-up the trajectories of the random dynamical system almost surely converge to one of the vertices of the simplex 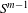$S^{m-1}$ , implying the survival of only one species. We also show that the minimal random point attractor of the system equals the set of all vertices. The convergence proof relies on a martingale-type limit theorem, which we prove in the appendix.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 1 , February 2017 , pp. 228 - 243
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnold, L.. Random Dynamical Systems. Springer, Berlin, 1998.CrossRefGoogle Scholar
Bernstein, S. N.. The solution of a mathematical problem related to the theory of heredity. Uchn. Zapiski NI Kaf. Ukr. Otd. Mat.(1) (1924), 83–115 (in Russian).Google Scholar
Chueshov, I. and Scheutzow, M.. On the structure of attractors and invariant measures for a class of monotone random systems. Dyn. Syst. 19 (2004), 127–144.CrossRefGoogle Scholar
Crauel, H.. Global random attractors are uniquely determined by attracting deterministic compact sets. Ann. Mat. Pura Appl. (4) 176 (1999), 57–72.Google Scholar
Crauel, H.. Random point attractors versus random set attractors. J. Lond. Math. Soc. (2) 63 (2001), 413–427.Google Scholar
Crauel, H., Dimitroff, G. and Scheutzow, M.. Criteria for strong and weak random attractors. J. Dynam. Differential Equations 21 (2009), 233–247.Google Scholar
Crauel, H. and Flandoli, F.. Attractors for random dynamical systems. Probab. Theory Related Fields 100 (1994), 365–393.Google Scholar
Ganikhodzhaev, N. N.. An application of the theory of Gibbs distributions to mathematical genetics. Dokl. Math. 61(3) (2000), 321–323.Google Scholar
Ganikhodzhaev, N. N.. The random models of heredity in the random environments. Dokl. Akad. Nauk RUz.(12) (2001), 6–8 (in Russian).Google Scholar
Ganikhodjaev, N. N., Ganikhodjaev, R. N. and Jamilov, U. U.. Quadratic stochastic operators and zero-sum game dynamics. Ergod. Th. & Dynam. Sys. (2014), doi:10.1017/etds.2013.109.Google Scholar
Ganikhodjaev, N. N., Jamilov, U. U. and Mukhitdinov, R. T.. On non-ergodic transformations on S 3 . J. Phys.: Conf. Ser. 435 (2013), 012005, doi:10.1088/1742-6596/435/1/012005.Google Scholar
Ganikhodjaev, N. N., Jamilov, U. U. and Mukhitdinov, R. T.. Non-ergodic quadratic operators of bisexual population. Ukrainian Math. J. 65(6) (2013), 1152–1160.Google Scholar
Ganikhodjaev, N. N. and Zanin, D. V.. On a necessary condition for the ergodicity of quadratic operators defined on the two-dimensional simplex. Russian Math. Surveys 59(3) (2004), 571–572.CrossRefGoogle Scholar
Ganikhodjaev, N. N. and Zanin, D. V.. Ergodic Volterra quadratic transformations of the simplex. Preprint, 2012, arXiv:1205.3841 (in Russian).Google Scholar
Ganikhodzhaev, R. N.. Quadratic stochastic operators, Lyapunov functions, and tournaments. Sb. Math. 76(2) (1993), 489–506.Google Scholar
Ganikhodzhaev, R. N.. Map of fixed points and Lyapunov functions for a class of discrete dynamical systems. Math. Notes 56(5) (1994), 1125–1131.Google Scholar
Ganikhodzhaev, R. N. and Eshmamatova, D. B.. Quadratic automorphisms of a simplex and the asymptotic behavior of their trajectories. Vladikavkaz. Mat. Zh. 8(2) (2006), 12–28 (in Russian).Google Scholar
Ganikhodzhaev, R. N., Mukhamedov, F. M. and Rozikov, U. A.. Quadratic stochastic operators and processes: results and open problems. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 14(2) (2011), 279–335.Google Scholar
Hall, P. and Heyde, C. C.. Martingale Limit Theory and its Application. Academic Press, New York, 1980.Google Scholar
Kesten, H.. Quadratic transformations: a model for population growth I. Adv. Appl. Probab. 2(1) (1970), 1–82.Google Scholar
Kesten, H.. Quadratic transformations: a model for population growth. II. Adv. Appl. Probab. 2(2) (1970), 179–228.Google Scholar
Krengel, U.. Einführung in die Wahrscheinlichkeitstheorie und Statistik, 6. Aufl. Vieweg, Braunschweig, 2002.Google Scholar
Lyubich, Yu. I.. Mathematical Structures in Population Genetics (Biomathematics, 22) . Springer, Berlin, 1992.Google Scholar
Mukhamedov, F., Akin, H. and Temir, S.. On infinite dimensional quadratic Volterra operators. J. Math. Anal. Appl. 310 (2005), 533–556.Google Scholar
Rozikov, U. A. and Jamilov, U. U.. F-quadratic stochastic operators. Math. Notes 83(4) (2008), 554–559.Google Scholar
Rozikov, U. A. and Jamilov, U. U.. The dynamics of strictly non-Volterra quadratic stochastic operators on the two-dimensional simplex. Sb. Math. 200(9) (2009), 1339–1351.Google Scholar
Rozikov, U. A. and Jamilov, U. U.. Volterra quadratic stochastic of a two-sex population. Ukrainian Math. J. 63(7) (2011), 1136–1153.Google Scholar
Scheutzow, M.. Comparison of various concepts of a random attractor: a case study. Arch. Math. 78 (2002), 233–240.Google Scholar
Scheutzow, M. and Steinsaltz, D.. Chasing balls through martingale fields. Ann. Probab. 30 (2002), 2046–2080.Google Scholar
Ulam, S. M.. A Collection of Mathematical Problems. Interscience, New York–London, 1960.Google Scholar
Vallander, S. S.. On the limit behavior of iteration sequences of certain quadratic transformations. Sovrem. Mat. Dokl. 13 (1972), 123–126.Google Scholar
Zakharevich, M. I.. On the behavior of trajectories and the ergodic hypothesis for quadratic mappings of a simplex. Russian Math. Surveys 33(6) (1978), 265–266.CrossRefGoogle Scholar