Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T09:58:17.718Z Has data issue: false hasContentIssue false
  • English
  • Français

On the distribution of orbits in affine varieties

Published online by Cambridge University Press:  03 July 2014

CLAYTON PETSCHE
CLAYTON PETSCHE*
Affiliation:
Department of Mathematics, Oregon State University, Corvallis, OR 97331, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given an affine variety 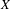$X$, a morphism 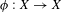${\it\phi}:X\rightarrow X$, a point 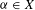${\it\alpha}\in X$, and a Zariski-closed subset $V$ of 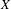$X$, we show that the forward 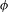${\it\phi}$-orbit of ${\it\alpha}$ meets $V$ in at most finitely many infinite arithmetic progressions, and the remaining points lie in a set of Banach density zero. This may be viewed as a weak asymptotic version of the dynamical Mordell–Lang conjecture for affine varieties. The results hold in arbitrary characteristic, and the proof uses methods of ergodic theory applied to compact Berkovich spaces.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 7 , October 2015 , pp. 2231 - 2241
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bell, J. P.. A generalised Skolem–Mahler–Lech theorem for affine varieties. J. Lond. Math. Soc. (2) 73 (2006), 367–379.CrossRefGoogle Scholar
Bell, J. P., Ghioca, D. and Tucker, T. J.. The dynamical Mordell–Lang problem for étale maps. Amer. J. Math. 132 (2010), 1655–1675.CrossRefGoogle Scholar
Bell, J. P., Ghioca, D. and Tucker, T. J.. The dynamical Mordell–Lang problem for Noetherian spaces. Preprint, 2014. http://arxiv.org/pdf/1401.6659v1.pdf.Google Scholar
Berkovich, V. G.. Spectral Theory and Analytic Geometry over Non-Archimedean Fields (Mathematical Surveys and Monographs, 33). American Mathematical Society, Providence, RI, 1990.Google Scholar
Bézivin, J. -P.. Suites récurrentes linéaires en caractéristique non nulle. Bull. Soc. Math. France 115 (1987), 227–239.CrossRefGoogle Scholar
Billingsley, P.. Convergence of Probability Measures, 2nd edn. John Wiley & Sons, New York, 1999.CrossRefGoogle Scholar
Denis, L.. Géométrie et suites récurrentes. Bull. Soc. Math. France 122 (1994), 13–27.CrossRefGoogle Scholar
Favre, C.. Dynamique des applications rationnelles. PhD Thesis, Université Paris-Sud, 2000.Google Scholar
Folland, G. B.. Real Analysis: Modern Techniques and Their Applications, 2nd edn. John Wiley & Sons, New York, 1999.Google Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.CrossRefGoogle Scholar
Furstenberg, H.. Poincaré recurrence and number theory. Bull. Amer. Math. Soc. (N.S.) 5 (1981), 211–234.CrossRefGoogle Scholar
Ghioca, D. and Tucker, T. J.. Periodic points, linearizing maps, and the dynamical Mordell–Lang problem. J. Number Theory 129 (2009), 1392–1403.CrossRefGoogle Scholar
Ghioca, D., Tucker, T. J. and Zieve, M. E.. Intersections of polynomials orbits, and a dynamical Mordell–Lang conjecture. Invent. Math. 171 (2008), 463–483.CrossRefGoogle Scholar
Gignac, W.. Measures and dynamics on Noetherian spaces. J. Geom. Anal. to appear. http://link.springer.com/article/10.1007/s12220-013-9394-9.Google Scholar
Gignac, W.. Equidistribution of preimages in nonarchimedean dynamics. PhD Thesis, University of Michigan, 2013, http://hdl.handle.net/2027.42/99809.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York, 1982.CrossRefGoogle Scholar