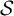Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T04:37:33.961Z Has data issue: false hasContentIssue false
  • English
  • Français

On the automorphism group of minimal $\mathcal {S}$-adic subshifts of finite alphabet rank

Part of: Topological dynamics

Published online by Cambridge University Press:  30 June 2021

BASTIÁN ESPINOZA  and
ALEJANDRO MAASS
BASTIÁN ESPINOZA*
Affiliation:
Departamento de Ingeniería Matemática and Centro de Modelamiento Matemático, Universidad de Chile & IRL-CNRS 2807, Beauchef 851, Santiago, Chile Laboratoire Amiénois de Mathématique Fondamentale et Appliquée, CNRS UMR 7352, Université de Picardie Jules Verne, 33 rue Saint Leu, 80039 Amiens cedex 1, France
ALEJANDRO MAASS
Affiliation:
Departamento de Ingeniería Matemática and Centro de Modelamiento Matemático, Universidad de Chile & IRL-CNRS 2807, Beauchef 851, Santiago, Chile (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It has been recently proved that the automorphism group of a minimal subshift with non-superlinear word complexity is virtually 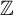$\mathbb {Z}$ [Cyr and Kra. The automorphism group of a shift of linear growth: beyond transitivity. Forum Math. Sigma3 (2015), e5; Donoso et al. On automorphism groups of low complexity subshifts. Ergod. Th. & Dynam. Sys.36(1) (2016), 64–95]. 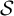In this article we extend this result to a broader class proving that the automorphism group of a minimal $\mathcal {S}$ -adic subshift of finite alphabet rank is virtually 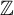$\mathbb {Z}$ . The proof is based on a fine combinatorial analysis of the asymptotic classes in this type of subshifts, which we prove are a finite number.

Keywords

S-adic subshiftsautomorphism groupminimal Cantor systemsfinite topological rank

MSC classification

Primary: 37B10: Symbolic dynamics
Secondary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 9 , September 2022 , pp. 2800 - 2822
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bezuglyi, S., Kwiatkowski, J., Medynets, K. and Solomyak, B.. Finite rank Bratteli diagrams: structure of invariant measures. Trans. Amer. Math. Soc. 365(5) (2013), 2637–2679.CrossRefGoogle Scholar
Boyle, M., Lind, D. and Rudolph, D.. The automorphism group of a shift of finite type. Trans. Amer. Math. Soc. 306(1) (1988), 71–114.CrossRefGoogle Scholar
Berthé, V., Steiner, W. and Thuswaldner, J. M.. Multidimensional continued fractions and symbolic codings of toral translations. Preprint, 2020, arXiv:2005.13038.Google Scholar
Berthé, V., Steiner, W., Thuswaldner, J. M. and Yassawi, R.. Recognizability for sequences of morphisms. Ergod. Th. & Dynam. Sys. 39(11) (2019), 2896–2931.CrossRefGoogle Scholar
Cyr, V. and Kra, B.. The automorphism group of a shift of linear growth: beyond transitivity. Forum Math. Sigma 3 (2015), e5.CrossRefGoogle Scholar
Cyr, V. and Kra, B.. The automorphism group of a minimal shift of stretched exponential growth. J. Mod. Dyn. 10 (2016), 483–495.Google Scholar
Cyr, V. and Kra, B.. The automorphism group of a shift of subquadratic growth. Proc. Amer. Math. Soc. 144(2) (2016), 613–621.CrossRefGoogle Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S.. On automorphism groups of low complexity subshifts. Ergod. Th. & Dynam. Sys. 36(1) (2016), 64–95.CrossRefGoogle Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S.. Interplay between finite topological rank minimal Cantor systems, ${\mathcal{S}}$ -adic subshifts and their complexity. Trans. Amer. Math. Soc. 374(5) (2021), 3453–3489.CrossRefGoogle Scholar
Durand, F., Frank, A. and Maass, A.. Eigenvalues of minimal Cantor systems. J. Eur. Math. Soc. (JEMS) 21(3) (2019), 727–775.CrossRefGoogle Scholar
Downarowicz, T. and Maass, A.. Finite-rank Bratteli–Vershik diagrams are expansive. Ergod. Th. & Dynam. Sys. 28(3) (2008), 739–747.CrossRefGoogle Scholar
Fiebig, D. and Fiebig, U.-R.. The automorphism group of a coded system. Trans. Amer. Math. Soc. 348(8) (1996), 3173–3191.CrossRefGoogle Scholar
Kim, K. H. and Roush, F. W.. On the automorphism groups of subshifts. Pure Math. Appl. Ser. B 1 (4) (1990), 203–230 (1991).Google Scholar
Lothaire, M.. Combinatorics on Words (Cambridge Mathematical Library). Cambridge University Press, Cambridge, 1997, with a foreword by Roger Lyndon and a preface by Dominique Perrin, Corrected reprint of the 1983 original, with a new preface by Perrin.CrossRefGoogle Scholar
Salo, V.. Toeplitz subshift whose automorphism group is not finitely generated. Colloq. Math. 146(1) (2017), 53–76.CrossRefGoogle Scholar