Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T00:36:01.722Z Has data issue: false hasContentIssue false
  • English
  • Français

On stable transitivity of finitely generated groups of volume-preserving diffeomorphisms

Published online by Cambridge University Press:  02 May 2017

ZHIYUAN ZHANG
ZHIYUAN ZHANG*
Affiliation:
Institut de Mathématique de Jussieu—Paris Rive Gauche, Bâtiment Sophie Germain, Bureau 652, 75205 Paris Cedex 13, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we provide a new criterion for the stable transitivity of volume-preserving finite generated groups on any compact Riemannian manifold. As one of our applications, we generalize a result of Dolgopyat and Krikorian [On simultaneous linearization of diffeomorphisms of the sphere. Duke Math. J. 136 (2007), 475–505] and obtain stable transitivity for random rotations on the sphere in any dimension. As another application, we show that for 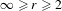$\infty \geq r\geq 2$, for any 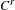$C^{r}$ volume-preserving partially hyperbolic diffeomorphism $g$ on any compact Riemannian manifold 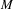$M$ having sufficiently Hölder stable or unstable distribution, for any sufficiently large integer 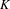$K$ and for any 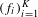$(f_{i})_{i=1}^{K}$ in a 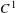$C^{1}$ open 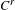$C^{r}$ dense subset of 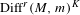$\text{Diff}^{r}(M,m)^{K}$, the group generated by 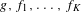$g,f_{1},\ldots ,f_{K}$ acts transitively.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 2 , February 2019 , pp. 554 - 576
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auerbach, H.. Sur les groupes linéaires bornés (III). Studia Math. 5 (1934), 43–49.Google Scholar
Avila, A., Crovisier, S. and Wilkinson, A.. Diffeomorphisms with positive metric entropy. Publ. Math. Inst. Hautes Études Sci. to appear.Google Scholar
Avila, A. and Viana, M.. Extremal Lyapunov exponents: an invariance principle and applications. Invent. Math. 181(1) (2010), 115–189.Google Scholar
Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158 (2004), 33–104.Google Scholar
Brown, A. and Rodriguez Hertz, F.. Measure rigidity for random dynamics on surfaces and related skew products. J. Amer. Math. Soc. to appear.Google Scholar
Burns, K., Dolgopyat, D., Pesin, Y. and Pollicott, M.. Stable ergodicity for partially hyperbolic attractors with negative central exponents. J. Mod. Dyn. 2 (2008), 63–81.Google Scholar
Dolgopyat, D.. On differentiability of SRB states for partially hyperbolic systems. Invent. Math. 155 (2004), 389–449.Google Scholar
Dolgopyat, D. and Krikorian, R.. On simultaneous linearization of diffeomorphisms of the sphere. Duke Math. J. 136 (2007), 475–505.Google Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583) . Springer, Berlin, 1977.Google Scholar
Koropecki, A. and Nassiri, M.. Transitivity of generic semigroups of area-preserving surface diffeomorphisms. Math. Z. 266(3) (2010), 707–718.Google Scholar
Liu, P.-D. and Qian, M.. Smooth Ergodic Theory of Random Dynamical Systems (Lecture Notes in Mathematics, 1606) . Springer, Berlin, 1995.Google Scholar
Nassiri, M. and Pujals, E.. Robust transitivity in Hamiltonian dynamics. Ann. Sci. Éc. Norm. Supér. 45 (2012), 191–239.Google Scholar
Pesin, Ya.. Families of invariant manifolds corresponding to nonzero characteristic exponents. Math. USSR-Izv. 40(6) (1976), 1261–1305.Google Scholar
Pugh, C., Shub, M. and Wilkinson, A.. Hölder foliations. Duke Math. J. 86(3) (1997), 517–546.Google Scholar