Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-06T13:06:37.812Z Has data issue: false hasContentIssue false
  • English
  • Français

On some generalizations of skew-shifts on 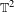$\mathbb{T}^{2}$

Published online by Cambridge University Press:  04 May 2017

KRISTIAN BJERKLÖV
KRISTIAN BJERKLÖV*
Affiliation:
Department of Mathematics, KTH Royal Institute of Technology, 100 44 Stockholm, Sweden email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we investigate maps of the two-torus 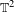$\mathbb{T}^{2}$ of the form 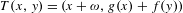$T(x,y)=(x+\unicode[STIX]{x1D714},g(x)+f(y))$ for Diophantine $\unicode[STIX]{x1D714}\in \mathbb{T}$ and for a class of maps 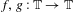$f,g:\mathbb{T}\rightarrow \mathbb{T}$, where each $g$ is strictly monotone and of degree 2 and each 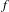$f$ is an orientation-preserving circle homeomorphism. For our class of 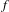$f$ and $g$, we show that $T$ is minimal and has exactly two invariant and ergodic Borel probability measures. Moreover, these measures are supported on two $T$-invariant graphs. One of the graphs is a strange non-chaotic attractor whose basin of attraction consists of (Lebesgue) almost all points in 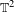$\mathbb{T}^{2}$. Only a low-regularity assumption (Lipschitz) is needed on the maps 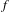$f$ and $g$, and the results are robust with respect to Lipschitz-small perturbations of 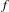$f$ and $g$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 1 , January 2019 , pp. 19 - 61
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A.. Global theory of one-frequency Schrödinger operators. Acta Math. 215(1) (2015), 1–54.Google Scholar
Avila, A. and Krikorian, R.. Monotonic cocycles. Invent. Math. 202(1) (2015), 271–331.Google Scholar
Benedicks, M. and Carleson, L.. The dynamics of the Hénon map. Ann. of Math. (2) 133(1) (1991), 73–169.Google Scholar
Bjerklöv, K.. Positive Lyapunov exponent and minimality for a class of one-dimensional quasi-periodic Schrödinger equations. Ergod. Th. & Dynam. Sys. 25(4) (2005), 1015–1045.Google Scholar
Bjerklöv, K.. Quasi-periodic perturbation of unimodal maps exhibiting an attracting 3-cycle. Nonlinearity 25(3) (2012), 683–741.Google Scholar
Bjerklöv, K.. The dynamics of a class of quasi-periodic Schrödinger cocycles. Ann. Henri Poincaré 16(4) (2015), 961–1031.Google Scholar
Bourgain, J., Goldstein, M. and Schlag, W.. Anderson localization for Schrödinger operators on ℤ with potentials given by the skew-shift. Comm. Math. Phys. 220(3) (2001), 583–621.Google Scholar
Bowen, R.. Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 153 (1971), 401–414.Google Scholar
Brin, M. and Stuck, G.. Introduction to Dynamical Systems. Cambridge University Press, Cambridge, 2002.Google Scholar
Collet, P. and Eckmann, J.-P.. On the abundance of aperiodic behaviour for maps on the interval. Comm. Math. Phys. 73(2) (1980), 115–160.Google Scholar
Dinaburg, E. I. and Sinai, Ja. G.. The one-dimensional Schrödinger equation with quasi-periodic potential. Funksional. Anal. i Prilozhen. 9(4) (1975), 8–21.Google Scholar
Fröhlich, J., Spencer, T. and Wittwer, P.. Localization for a class of one-dimensional quasi-periodic Schrödinger operators. Comm. Math. Phys. 132(1) (1990), 5–25.Google Scholar
Herman, M. R.. Construction d’un difféomorphisme minimal d’entropie topologique non nulle. Ergod. Th. & Dynam. Sys. 1(1) (1981), 65–76.Google Scholar
Herman, M. R.. Une méthode pour minorer les exposants de Lyapounov et quelques exemples montrant le caractère local d’un théorème d’Arnold et de Moser sur le tore de dimension 2. Comment. Math. Helv. 58(3) (1983), 453–502.Google Scholar
Jäger, T.. Strange non-chaotic attractors in quasiperiodically forced circle maps. Comm. Math. Phys. 289(1) (2009), 253–289.Google Scholar
Jäger, T.. Strange non-chaotic attractors in quasi-periodically forced circle maps: Diophantine forcing. Ergod. Th. & Dynam. Sys. 33(5) (2013), 1477–1501.Google Scholar
Jakobson, M. V.. Absolutely continuous invariant measures for one-parameter families of one-dimensional maps. Comm. Math. Phys. 81(1) (1981), 39–88.Google Scholar
Johnson, R. A.. Ergodic theory and linear differential equations. J. Differential Equations 28(1) (1978), 23–34.Google Scholar
Jorba, A., Tatjer, J. C., Nunez, C. and Obaya, R.. Old and new results on strange nonchaotic attractors. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 17(11) (2007), 3895–3928.Google Scholar
Kim, J.-W., Kim, S.-Y., Hunt, B. and Ott, E.. Fractal properties of robust strange nonchaotic attractors in maps of two or more dimensions. Phys. Rev. E 67(3) (2003), 036211, 8 pp.Google Scholar
Oseledec, V. I.. A multiplicative ergodic theorem: characteristic Ljapunov exponents of dynamical systems. Tr. Mosk. Mat. Obs. 19 (1968), 179–210.Google Scholar
Puig, J.. Cantor spectrum for the almost Mathieu operator. Comm. Math. Phys. 244(2) (2004), 297–309.Google Scholar
Sinai, Y. G.. Anderson localization for one-dimensional difference Schrödinger operator with quasiperiodic potential. J. Stat. Phys. 46(5–6) (1987), 861–909.Google Scholar
Sorets, E. and Spencer, T.. Positive Lyapunov exponents for Schrödinger operators with quasi-periodic potentials. Comm. Math. Phys. 142(3) (1991), 543–566.Google Scholar
Wang, Y. and Zhang, Z.. Uniform positivity and continuity of Lyapunov exponents for a class of C 2 quasiperiodic Schrödinger cocycles. J. Funct. Anal. 268(9) (2015), 2525–2585.Google Scholar
Wang, Y. and Zhang, Z.. Cantor spectrum for a class of C 2 quasiperiodic Schrödinger operators. Int. Math. Res. Not. IMRN, to appear.Google Scholar
Young, L.-S.. Some open sets of nonuniformly hyperbolic cocycles. Ergod. Th. & Dynam. Sys. 13(2) (1993), 409–415.Google Scholar
Young, L.-S.. Lyapunov exponents for some quasi-periodic cocycles. Ergod. Th. & Dynam. Sys. 17(2) (1997), 483–504.Google Scholar