No CrossRef data available.
Article contents
On intrinsic ergodicity of factors of 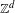 $\mathbb{Z}^{d}$ subshifts
$\mathbb{Z}^{d}$ subshifts
Published online by Cambridge University Press: 06 October 2015
Abstract
It is well known that any  $\mathbb{Z}$ subshift with the specification property has the property that every factor is intrinsically ergodic, i.e. every factor has a unique factor of maximal entropy. In recent work, other
$\mathbb{Z}$ subshift with the specification property has the property that every factor is intrinsically ergodic, i.e. every factor has a unique factor of maximal entropy. In recent work, other  $\mathbb{Z}$ subshifts have been shown to possess this property as well, including
$\mathbb{Z}$ subshifts have been shown to possess this property as well, including  $\unicode[STIX]{x1D6FD}$-shifts and a class of
$\unicode[STIX]{x1D6FD}$-shifts and a class of  $S$-gap shifts. We give two results that show that the situation for
$S$-gap shifts. We give two results that show that the situation for 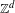 $\mathbb{Z}^{d}$ subshifts with
$\mathbb{Z}^{d}$ subshifts with 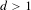 $d>1$ is quite different. First, for any
$d>1$ is quite different. First, for any 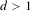 $d>1$, we show that any
$d>1$, we show that any 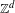 $\mathbb{Z}^{d}$ subshift possessing a certain mixing property must have a factor with positive entropy which is not intrinsically ergodic. In particular, this shows that for
$\mathbb{Z}^{d}$ subshift possessing a certain mixing property must have a factor with positive entropy which is not intrinsically ergodic. In particular, this shows that for 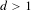 $d>1$,
$d>1$, 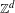 $\mathbb{Z}^{d}$ subshifts with specification cannot have all factors intrinsically ergodic. We also give an example of a
$\mathbb{Z}^{d}$ subshifts with specification cannot have all factors intrinsically ergodic. We also give an example of a 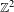 $\mathbb{Z}^{2}$ shift of finite type, introduced by Hochman, which is not even topologically mixing, but for which every positive-entropy subshift factor is intrinsically ergodic.
$\mathbb{Z}^{2}$ shift of finite type, introduced by Hochman, which is not even topologically mixing, but for which every positive-entropy subshift factor is intrinsically ergodic.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2015



