Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Glasner, Eli
and
Megrelishvili, Michael
2013.
Asymptotic Geometric Analysis.
Vol. 68,
Issue. ,
p.
75.
Glasner, Eli
and
Megrelishvili, Michael
2014.
Recent Progress in General Topology III.
p.
399.
Ben Yaacov, Itaï
Ibarlucía, Tomás
and
Tsankov, Todor
2017.
Eberlein oligomorphic groups.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 3,
p.
2181.
Glasner, Eli
and
Megrelishvili, Michael
2018.
Ergodic Theory and Dynamical Systems in their Interactions with Arithmetics and Combinatorics.
Vol. 2213,
Issue. ,
p.
351.


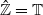 , and which is
, and which is 