Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T08:23:44.319Z Has data issue: false hasContentIssue false
  • English
  • Français

On density of ergodic measures and generic points

Published online by Cambridge University Press:  08 November 2016

KATRIN GELFERT  and
DOMINIK KWIETNIAK
KATRIN GELFERT
Affiliation:
Institute of Mathematics, Federal University of Rio de Janeiro, Cidade Universitaria – Ilha do Fundão, Rio de Janeiro 21945-909, Brazil email [email protected]
DOMINIK KWIETNIAK
Affiliation:
Institute of Mathematics, Federal University of Rio de Janeiro, Cidade Universitaria – Ilha do Fundão, Rio de Janeiro 21945-909, Brazil email [email protected] Faculty of Mathematics and Computer Science, Jagiellonian University in Krakow, ul. Łojasiewicza 6, 30-348 Kraków, Poland email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce two properties of dynamical systems on Polish metric spaces: closeability and linkability. We show that they imply density of ergodic measures in the space of invariant probability measures and the existence of a generic point for every invariant measure. In the compact case, it follows from our conditions that the set of invariant measures is either a singleton of a measure concentrated on a periodic orbit or the Poulsen simplex. We provide examples showing that closability and linkability are independent properties. 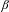Our theory applies to systems with the periodic specification property, irreducible Markov chains over a countable alphabet, certain coded systems including $\unicode[STIX]{x1D6FD}$-shifts and $S$-gap shifts, 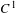$C^{1}$-generic diffeomorphisms of a compact manifold 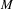$M$ and certain geodesic flows of a complete connected negatively curved manifold.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 5 , August 2018 , pp. 1745 - 1767
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdenur, F., Bonatti, Ch., Crovisier, S., Díaz, L. J. and Wen, L.. Periodic points and homoclinic classes. Ergod. Th. & Dynam. Sys. 27 (2007), 1–22.Google Scholar
Abdenur, F., Bonatti, Ch. and Crovisier, S.. Nonuniform hyperbolicity for C 1 -generic diffeomorphisms. Israel J. Math. 183 (2011), 1–60.Google Scholar
Aliprantis, C. D. and Border, K. C.. Infinite Dimensional Analysis (A Hitchhiker’s Guide) , 3rd edn. Springer, Berlin, 2006.Google Scholar
Bowen, R.. Periodic points and measures for Axiom A diffeomorphisms. Trans. Amer. Math. Soc. 154 (1971), 377–397.Google Scholar
Buzzi, J.. Specification on the interval. Trans. Amer. Math. Soc. 349 (1997), 2737–2754.Google Scholar
Vaughn Climenhaga’s Math Blog (accessed 24 March 2014) http://vaughnclimenhaga.wordpress.com/2012/04/18/a-useful-example-for-the-space-of-ergodic-measures/.Google Scholar
Climenhaga, V. and Thompson, D. J.. Intrinsic ergodicity beyond specification: 𝛽-shifts, S-gap shifts, and their factors. Israel J. Math. 192 (2012), 785–817.Google Scholar
Coudene, Y.. Topological dynamics and local product structure. J. Lond. Math. Soc. (2) 69 (2004), 441–456.Google Scholar
Coudene, Y. and Schapira, B.. Generic measures for hyperbolic flows on non-compact spaces. Israel J. Math. 179 (2010), 157–172.Google Scholar
Denker, M., Grillenberger, Ch. and Sigmund, K.. Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527) . Springer, New York.Google Scholar
Downarowicz, T.. The Choquet simplex of invariant measures for minimal flows. Israel J. Math. 74 (1991), 241–256.Google Scholar
Downarowicz, T.. Entropy in Dynamical Systems (New Mathematical Monographs, 18) . Cambridge University Press, Cambridge, 2011.CrossRefGoogle Scholar
Downarowicz, T. and Serafin, J.. Possible entropy functions. Israel J. Math. 135 (2003), 221–250.Google Scholar
Dudley, R. M.. Real Analysis and Probability (Cambridge Studies in Advanced Mathematics, 74) . Cambridge University Press, Cambridge, 2002, Revised reprint of the 1989 original.Google Scholar
Greschonig, G. and Schmidt, K.. Ergodic decomposition of quasi-invariant probability measures. Colloq. Math. 84/85(part 2) (2000), 495–514, Dedicated to the memory of Anzelm Iwanik.CrossRefGoogle Scholar
Grivaux, S. and Matheron, É.. Invariant measures for frequently hypercyclic operators. Adv. Math. 265 (2014), 371–427.CrossRefGoogle Scholar
Jung, U.. On the existence of open and bi-continuing codes. Trans. Amer. Math. Soc. 363 (2011), 1399–1417.Google Scholar
Kwietniak, D., Ła̧cka, M. and Oprocha, P.. A panorama of specification-like properties and their consequences. Dynamics and Numbers (Contemporary Mathematics, 669) . American Mathematical Society, Providence, RI, 2016, pp. 155–186.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Lindenstrauss, J., Olsen, G. and Sternfeld, Y.. The Poulsen simplex. Ann. Inst. Fourier (Grenoble) 28 (1978), vi, 91–114.Google Scholar
Parthasarathy, K. R.. On the category of ergodic measures. Illinois J. Math. 5 (1961), 648–656.Google Scholar
Petersen, K.. Chains, entropy, coding. Ergod. Th. & Dynam. Sys. 6 (1986), 415–448.Google Scholar
Pfister, C.-E. and Sullivan, W. G.. Large deviations estimates for dynamical systems without the specification property. Applications to the 𝛽-shifts. Nonlinearity 18 (2005), 237–261.Google Scholar
Poulsen, E. T.. A simplex with dense extreme points. Ann. Inst. Fourier (Grenoble) 11 (1961), 83–87, XIV.Google Scholar
Simon, B.. Convexity. An Analytic Viewpoint (Cambridge Tracts in Mathematics, 187) . Cambridge University Press, Cambridge, 2011.CrossRefGoogle Scholar
Sigmund, K.. Generic properties of invariant measures for Axiom A diffeomorphisms. Invent. Math. 11 (1970), 99–109.Google Scholar
Sigmund, K.. On dynamical systems with the specification property. Trans. Amer. Math. Soc. 190 (1974), 285–299.Google Scholar
Sun, W. X. and Tian, X. T.. The structure on invariant measures of C 1 generic diffeomorphisms. Acta Math. Sin. (Engl. Ser.) 28 (2012), 817–824.Google Scholar
Thomsen, K.. On the structure of beta shifts. Algebraic and Topological Dynamics (Contemporary Mathematics, 385) . American Mathematical Society, Providence, RI, 2005, pp. 321–332.Google Scholar
Thomsen, K.. On the ergodic theory of synchronized systems. Ergod. Th. & Dynam. Sys. 26 (2006), 1235–1256.Google Scholar
Ville, J.. Étude critique de la notion de collectif, Vol. 218. Theses françaises de lentre-deux-guerres, Paris, 1939.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar