Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-17T02:12:12.704Z Has data issue: false hasContentIssue false
  • English
  • Français

Odd-symplectic forms via surgery and minimality in symplectic dynamics

Published online by Cambridge University Press:  05 September 2018

HANSJÖRG GEIGES Open the ORCID record for HANSJÖRG GEIGES [Opens in a new window]  and
KAI ZEHMISCH
HANSJÖRG GEIGES
Affiliation:
Mathematisches Institut, Universität zu Köln, Weyertal 86–90, 50931 Köln, Germany email [email protected]
KAI ZEHMISCH
Affiliation:
Mathematisches Institut, Universität Gießen, Arndtstraße 2, 35392 Gießen, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct an infinite family of odd-symplectic forms (also known as Hamiltonian structures) on the $3$-sphere 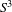$S^{3}$ that do not admit a symplectic cobordism to the standard contact structure on 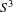$S^{3}$. This answers in the negative a question raised by Joel Fish motivated by the search for minimal characteristic flows.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 3 , March 2020 , pp. 699 - 713
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, L., Hahn, F. and Markus, L.. Minimal flows on nilmanifolds. Flows on Homogeneous Spaces (Annals of Mathematics Studies, 53) . Eds. Auslander, L., Green, L. and Hahn, F.. Princeton University Press, Princeton, NJ, 1963.Google Scholar
Bramham, B. and Hofer, H.. First Steps Towards a Symplectic Dynamics (Surveys in Differential Geometry, 17) . International Press, Boston, 2012, pp. 127–177.Google Scholar
Cieliebak, K. and Volkov, E.. First steps in Hamiltonian topology. J. Eur. Math. Soc. (JEMS) 17 (2015), 321–404.Google Scholar
Ding, F., Geiges, H. and Stipsicz, A. I.. Surgery diagrams for contact 3-manifolds. Turkish J. Math. 28 (2004), 41–74.Google Scholar
Eliashberg, Ya.. Topological characterization of Stein manifolds of dimension >2. Internat. J. Math. 1 (1990), 29–46.2.+Internat.+J.+Math.+1+(1990),+29–46.>Google Scholar
Eliashberg, Ya.. A few remarks about symplectic filling. Geom. Topol. 8 (2004), 277–293.Google Scholar
Eliashberg, Ya. and Fraser, M.. Topologically trivial Legendrian knots. J. Symplectic Geom. 7 (2009), 77–127.Google Scholar
Etnyre, J. B. and Honda, K.. Knots and contact geometry I: Torus knots and the figure eight knot. J. Symplectic Geom. 1 (2001), 63–120.Google Scholar
Etnyre, J. B. and Honda, K.. On symplectic cobordisms. Math. Ann. 323 (2002), 31–39.Google Scholar
Fish, J. W.. Feral pseudoholomorphic curves and minimal sets. Oberwolfach Rep. 12 (2015), 1941.Google Scholar
Geiges, H.. Contact Dehn surgery, symplectic fillings, and Property P for knots. Expo. Math. 24 (2006), 273–280.Google Scholar
Geiges, H.. An Introduction to Contact Topology (Cambridge Studies in Advanced Mathematics, 109) . Cambridge University Press, Cambridge, 2008.Google Scholar
Geiges, H. and Onaran, S.. Legendrian rational unknots in lens spaces. J. Symplectic Geom. 13 (2015), 17–50.Google Scholar
Geiges, H., Röttgen, N. and Zehmisch, K.. From a Reeb orbit trap to a Hamiltonian plug. Arch. Math. (Basel) 107 (2016), 397–404.Google Scholar
Geiges, H. and Zehmisch, K.. How to recognize a 4-ball when you see one. Münster J. Math. 6 (2013), 525–554.Google Scholar
Geiges, H. and Zehmisch, K.. Cobordisms between symplectic fibrations. Manuscripta Math. 153 (2017), 331–340.Google Scholar
Ghys, É.. Dynamique des flots unipotents sur les espaces homogènes. Séminaire Bourbaki 1991/92, Exp. No. 747 (Astérisque, 206) . Société Mathématique de France, Paris, 1992, pp. 93–136.Google Scholar
Ginzburg, V. L.. Calculation of contact and symplectic cobordism groups. Topology 31 (1992), 767–773.Google Scholar
Ginzburg, V. L.. An embedding S 2n-1→ℝ2n , 2n - 1 ≥ 7, whose Hamiltonian flow has no periodic trajectories. Int. Math. Res. Not. IMRN 1995 (1995), 83–97.Google Scholar
Ginzburg, V. L.. A smooth counterexample to the Hamiltonian Seifert conjecture in ℝ6 . Int. Math. Res. Not. IMRN 1997 (1997), 641–650.Google Scholar
Gompf, R. E.. Handlebody construction of Stein surfaces. Ann. of Math. (2) 148 (1998), 619–693.Google Scholar
Gompf, R. E. and Stipsicz, A. I.. 4-Manifolds and Kirby Calculus (Graduate Studies in Mathematics, 20) . American Mathematical Society, Providence, RI, 1999.Google Scholar
Herman, M.. Some open problems in dynamical systems. Proceedings of the International Congress of Mathematicians, Vol. II (Berlin, 1998) (Doc. Math., Extra Vol. II) . Deutsche Mathematiker-Vereinigung, Bielefeld, 1998, pp. 797–808.Google Scholar
Herman, M. R.. Examples of compact hypersurfaces in ℝ2p , 2p ≥ 6, with no periodic orbits. Hamiltonian Systems with Three or More Degrees of Freedom (NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 553) . Kluwer, Dordrecht, 1999, p. 126.Google Scholar
Herman, M. R.. Examples of compact hypersurfaces in $\mathbb{R}^{2p}$ , $2p\geq 6$ , with no periodic orbits, with comments by F. Laudenbach, available at https://www.college-de-france.fr/media/jean-christophe-yoccoz/UPL7089_herman_hypersurf.pdf.Google Scholar
Hofer, H.. Pseudoholomorphic curves in symplectizations with applications to the Weinstein conjecture in dimension three. Invent. Math. 114 (1993), 515–563.Google Scholar
Markus, L.. Lectures in Differentiable Dynamics. American Mathematical Society, Providence, RI, 1971.Google Scholar
McDuff, D.. Symplectic manifolds with contact type boundaries. Invent. Math. 103 (1991), 651–671.Google Scholar
Weinstein, A.. Contact surgery and symplectic handlebodies. Hokkaido Math. J. 20 (1991), 241–251.Google Scholar