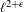Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bissacot, Rodrigo
Endo, Eric O.
van Enter, Aernout C. D.
and
Le Ny, Arnaud
2018.
Entropic Repulsion and Lack of the g-Measure Property for Dyson Models.
Communications in Mathematical Physics,
Vol. 363,
Issue. 3,
p.
767.
Endo, Eric O.
van Enter, Aernout C. D.
and
Le Ny, Arnaud
2021.
In and Out of Equilibrium 3: Celebrating Vladas Sidoravicius.
Vol. 77,
Issue. ,
p.
371.
GALLESCO, CHRISTOPHE
and
TAKAHASHI, DANIEL Y.
2022.
Mixing rates for potentials of non-summable variations.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 9,
p.
2823.
Chazottes, Jean-René
Gallo, Sandro
and
Takahashi, Daniel Y.
2023.
Gaussian concentration bounds for stochastic chains of unbounded memory.
The Annals of Applied Probability,
Vol. 33,
Issue. 5,
Berger, Noam
Conache, Diana
Johansson, Anders
and
Öberg, Anders
2025.
Uniqueness and mixing properties of Doeblin measures.
Probability Theory and Related Fields,