Article contents
Non-stationary smooth geometric structures for contracting measurable cocycles
Published online by Cambridge University Press: 28 June 2017
Abstract
We implement a differential-geometric approach to normal forms for contracting measurable cocycles to 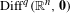 $\operatorname{Diff}^{q}(\mathbb{R}^{n},\mathbf{0})$,
$\operatorname{Diff}^{q}(\mathbb{R}^{n},\mathbf{0})$, 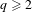 $q\geq 2$. We obtain resonance polynomial normal forms for the contracting cocycle and its centralizer, via
$q\geq 2$. We obtain resonance polynomial normal forms for the contracting cocycle and its centralizer, via 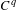 $C^{q}$ changes of coordinates. These are interpreted as non-stationary invariant differential-geometric structures. We also consider the case of contracted foliations in a manifold, and obtain
$C^{q}$ changes of coordinates. These are interpreted as non-stationary invariant differential-geometric structures. We also consider the case of contracted foliations in a manifold, and obtain 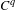 $C^{q}$ homogeneous structures on leaves for an action of the group of subresonance polynomial diffeomorphisms together with translations.
$C^{q}$ homogeneous structures on leaves for an action of the group of subresonance polynomial diffeomorphisms together with translations.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 2
- Cited by


