Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:40:50.440Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-smooth saddle-node bifurcations I: existence of an SNA

Published online by Cambridge University Press:  02 December 2014

GABRIEL FUHRMANN
GABRIEL FUHRMANN*
Affiliation:
Emmy Noether Group: Low-dimensional and Nonautonomous Dynamics, TU-Dresden, Dresden, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study one-parameter families of quasi-periodically forced monotone interval maps and provide sufficient conditions for the existence of a parameter at which the respective system possesses a non-uniformly hyperbolic attractor. This is equivalent to the existence of a sink-source orbit, that is, an orbit with positive Lyapunov exponent both forwards and backwards in time. The attractor itself is a non-continuous invariant graph with negative Lyapunov exponent, often referred to as ‘SNA’. In contrast to former results in this direction, our conditions are 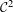${\mathcal{C}}^{2}$-open in the fibre maps. By applying a general result about saddle-node bifurcations in skew-products, we obtain a conclusion on the occurrence of non-smooth bifurcations in the respective families. Explicit examples show the applicability of the derived statements.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 4 , June 2016 , pp. 1130 - 1155
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anagnostopoulou, V. and Jäger, T.. Nonautonomous saddle-node bifurcations: Random and deterministic forcing. J. Differential Equations 253(2) (2012), 379–399.CrossRefGoogle Scholar
Arnold, L.. Random Dynamical Systems. Springer, Berlin, 1998.CrossRefGoogle Scholar
Bjerklöv, K.. Dynamics of the quasi-periodic Schrödinger cocycle at the lowest energy in the spectrum. Comm. Math. Phys. 272 (2007), 397–442, doi:101007/s00220-007-0238-y.CrossRefGoogle Scholar
Bjerklöv, K. and Saprykina, M.. Universal asymptotics in hyperbolicity breakdown. Nonlinearity 21(3) (2008), 557–586, QC 20100525.Google Scholar
Crucifix, M.. Why could ice ages be unpredictable? Clim. Past 9 (2013), 1053–1098.Google Scholar
Fuhrmann, G., Gröger, M. and Jäger, T.. Non-smooth saddle-node bifurcations II: Dimensions of the SNA, in preparation, 2014.Google Scholar
Glendinning, P.. The nonsmooth pitchfork bifurcation. Discrete Contin. Dyn. Syst. Ser. B. 2004, pp. 457–464.Google Scholar
Grebogi, C., Ott, E., Pelikan, S. and Yorke, J. A.. Strange attractors that are not chaotic. Phys. D 13 (1984), 261–268.Google Scholar
Gröger, M. and Jäger, T.. Dimensions of attractors in pinched skew products. Comm. Math. Phys. 320(1) (2013), 101–119.Google Scholar
Haro, A. and de la Llave, R.. Manifolds on the verge of a hyperbolicity breakdown. Chaos 16(1) (2006), 013120.Google Scholar
Herman, M.. Une méthode pour minorer les exposants de Lyapounov et quelques exemples montrant le caractère local d’un théorème d’Arnold et de Moser sur le tore de dimension 2. Comment. Math. Helv. 58 (1983), 453–502, doi:101007/BF02564647.Google Scholar
Jäger, T.. The creation of strange non-chaotic attractors in non-smooth saddle-node bifurcations. Mem. Amer. Math. Soc. 201 (2009), 1–106.Google Scholar
Jäger, T.. On the structure of strange non-chaotic attractors in pinched skew products. Ergod. Th. & Dynam. Sys. 27 (2007), 493–510.Google Scholar
Jäger, T.. Quasiperiodically forced interval maps with negative schwarzian derivative. Nonlinearity 16(4) (2003), 1239–1255.Google Scholar
Jäger, T.. Strange non-chaotic attractors in quasiperiodically forced circle maps. Comm. Math. Phys. 289 (2009), 253–289, doi:10.1007/s00220-009-0753-0.Google Scholar
Keller, G.. A note on strange nonchaotic attractors. Fund. Math. 151 (1996), 139–148.Google Scholar
Kim, J. and Kim, Y.. Strange nonchaotic attractors in quasiperiodically driven Izhikevich neuron models. J. Korean Phys. Soc. 60(4) (2012), 660–664.Google Scholar
Millions̆c̆ikov, V.. Proof of the existence of irregular systems of linear differential equations with quasi periodic coefficients. Differ. Uravn. 5(11) (1969), 1979–1983.Google Scholar
Nguyen, T., Doan, T., Jäger, T. and Siegmund, S.. Saddle-node bifurcations in the quasiperiodically forced logistic map. Internat. J. Bifur. Chaos 21 (2011), 1427–1438.Google Scholar
Núñez, C. and Obaya, R.. A non-autonomous bifurcation theory for deterministic scalar differential equations. Discrete Contin. Dyn. Syst. Ser. B 9 (2008), 701–730.Google Scholar
Osinga, H., Wiersig, J., Glendinning, P. and Feudel, U.. Multistability and nonsmooth bifurcations in the quasiperiodically forced circle map. Internat. J. Bifur. Chaos 11 (2001), 3085–3105.Google Scholar
Pötsche, C.. Bifurcations in Nonautonomous Dynamical Systems: Results and Tools in Discrete Time. Servizo de Publicacións da Universidade de Vigo, Vigo, 2011, pp. 163–212.Google Scholar
Sonechkin, D. and Ivachtchenko, N.. On the role of quasiperiodic forcing in the interannual and interdecadal climate variations. CLIVAR Exchanges 6 (2001), 5–6.Google Scholar
Stark, J.. Transitive sets for quasi-periodically forced monotone maps. Dyn. Syst. 18(4) (2003), 351–364.Google Scholar
Veraart, A. J., Faassen, E. J. , Dakos, V., van Nes, E. H. , Lürling, M. and Scheffer, M.. Recovery rates reflect distance to a tipping point in a living system. Nature 481 (2012), 357–359.Google Scholar
Vinograd, R.. A problem suggested by N. R. Erugin. Differ. Uravn. 11(4) (1975), 632–638.Google Scholar
Young, L.-S.. Lyapunov exponents for some quasi-periodic cocycles. Ergod. Th. & Dynam. Sys. 17 (1997), 483–504.CrossRefGoogle Scholar