Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T09:33:39.415Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-recurrence sets for weakly mixing linear dynamical systems

Published online by Cambridge University Press:  24 August 2012

SOPHIE GRIVAUX
SOPHIE GRIVAUX*
Affiliation:
CNRS, Laboratoire Paul Painlevé, UMR 8524, Université Lille 1, Cité Scientifique, 59655 Villeneuve d’Ascq Cedex, France (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study non-recurrence sets for weakly mixing dynamical systems by using linear dynamical systems. These are systems consisting of a bounded linear operator acting on a separable complex Banach space 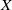$X$, which becomes a probability space when endowed with a non-degenerate Gaussian measure. We generalize some recent results of Bergelson, del Junco, Lemańczyk and Rosenblatt, and show in particular that sets 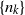$\{n_{k}\}$ such that 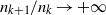$n_{k+1}/n_{k}\to +\infty $, or such that 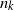$n_{k}$ divides 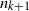$n_{k+1}$ for each 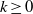$k\ge 0$, are non-recurrence sets for weakly mixing linear dynamical systems. We also give examples, for each 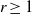$r\ge 1$, of $r$-Bohr sets which are non-recurrence sets for some weakly mixing systems.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 1 , February 2014 , pp. 132 - 152
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Badea, C. and Grivaux, S.. Unimodular eigenvalues, uniformly distributed sequences and linear dynamics. Adv. Math. 211 (2007), 766–793.Google Scholar
[2]Badea, C. and Grivaux, S.. Size of the peripheral point spectrum under power or resolvent growth conditions. J. Funct. Anal. 246 (2007), 302–329.Google Scholar
[3]Bayart, F. and Grivaux, S.. Frequently hypercyclic operators. Trans. Amer. Math. Soc. 358 (2006), 5083–5117.Google Scholar
[4]Bayart, F. and Grivaux, S.. Invariant Gaussian measures for operators on Banach spaces and linear dynamics. Proc. Lond. Math. Soc. 94 (2007), 181–210.Google Scholar
[5]Bayart, F. and Matheron, É.. Dynamics of Linear Operators, Vol. 179. Cambridge University Press, 2009.Google Scholar
[6]Bayart, F. and Matheron, É.. Mixing operators and small subsets of the circle. Preprint, 2011, arXiv:1112.1289.Google Scholar
[7]Bergelson, V., Del Junco, A., Lemańczyk, M. and Rosenblatt, J.. Rigidity and non-recurrence along sequences. Preprint, 2011, arXiv:1103.0905.Google Scholar
[8]Bonilla, A. and Grosse-Erdmann, K.-G.. On a theorem of Godefroy and Shapiro. Integral Equations Operator Theory 56 (2006), 151–162.Google Scholar
[9]Boshernitzan, M. and Glasner, E.. On two recurrence problems. Fund. Math. 206 (2009), 2013–2052.Google Scholar
[10]de Mathan, B.. Sur un problème de densité modulo 1. C. R. Acad. Sci. Paris 287 (1978), 277–279.Google Scholar
[11]Eisner, T. and Grivaux, S.. Hilbertian Jamison sequences and rigid dynamical systems. J. Funct. Anal. 261 (2011), 302–329.Google Scholar
[12]Flytzanis, E.. Unimodular eigenvalues and linear chaos in Hilbert spaces. Geom. Funct. Anal. 5 (1995), 1–13.CrossRefGoogle Scholar
[13]Furstenberg, H. and Weiss, B.. The finite multipliers of infinite ergodic transformations. The Structure of Attractors in Dynamical Systems (Proc. Conf., North Dakota State University, Fargo, ND, 1977) (Lecture Notes in Mathematics, 668). Springer, Berlin, 1978, pp. 127–132.Google Scholar
[14]Furstenberg, H.. Poincaré recurrence and number theory. Bull. Amer. Math. Soc. 5 (1981), 211–234.Google Scholar
[15]Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.Google Scholar
[16]Glasner, E.. On minimal actions of Polish groups. Topology Appl. 85 (1998), 119–125.Google Scholar
[17]Glasner, E.. Classifying dynamical systems by their recurrence properties. Topol. Methods Nonlinear Anal. 24 (2004), 21–40.Google Scholar
[18]Glasner, E. and Weiss, B.. On the interplay between measurable and topological dynamics. Handbook of Dynamical Systems, Vol. 1B. Ed. Hasselblatt et al, B., Elsevier, Amsterdam, 2006, pp. 597–648.Google Scholar
[19]Grivaux, S.. A new class of frequently hypercyclic operators. Indiana Univ. Math. J. to appear.Google Scholar
[20]Grivaux, S. and Roginskaya, M.. Some new examples of recurrence and non-recurrence sets for products of rotations on the unit circle. Preprint, 2012, arXiv:1202.3113.Google Scholar
[21]Jamison, B.. Eigenvalues of modulus 1. Proc. Amer. Math. Soc. 16 (1965), 375–377.Google Scholar
[22]Kalish, G.. On operators on separable Banach spaces with arbitrary prescribed point spectrum. Proc. Amer. Math. Soc. 34 (1972), 207–208.Google Scholar
[23]Katznelson, Y.. Chromatic numbers of Cayley graphs on $\mathbb {Z}$ and recurrence, Paul Erdoös and his mathematics (Budapest 1999). Combinatorica 21 (2001), 211–219.Google Scholar
[24]Pollington, A. D.. On the density of sequences $(n_k\xi )$. Illinois J. Math 23 (1979), 511–515.Google Scholar
[25]Ransford, T.. Eigenvalues and power growth. Israel J. Math. 146 (2005), 93–110.CrossRefGoogle Scholar
[26]Ransford, T. and Roginskaya, M.. Point spectra of partially power-bounded operators. J. Funct. Anal. 230 (2006), 432–445.Google Scholar
[27]Veech, W. A.. The equicontinuous structure relation for minimal abelian transformation groups. Amer. J. Math. 90 (1968), 723–732.Google Scholar