Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T18:06:48.183Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-negative integral matrices with given spectral radius and controlled dimension

Part of: Topological dynamics Special matrices Basic linear algebra

Published online by Cambridge University Press:  21 September 2021

MEHDI YAZDI Open the ORCID record for MEHDI YAZDI [Opens in a new window]
MEHDI YAZDI*
Affiliation:
Mathematical Institute, University of Oxford, Woodstock Road, Oxford OX2 6GG, UK
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A celebrated theorem of Douglas Lind states that a positive real number is equal to the spectral radius of some integral primitive matrix, if and only if, it is a Perron algebraic integer. Given a Perron number p, we prove that there is an integral irreducible matrix with spectral radius p, and with dimension bounded above in terms of the algebraic degree, the ratio of the first two largest Galois conjugates, and arithmetic information about the ring of integers of its number field. This arithmetic information can be taken to be either the discriminant or the minimal Hermite-like thickness. Equivalently, given a Perron number p, there is an irreducible shift of finite type with entropy 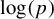$\log (p)$ defined as an edge shift on a graph whose number of vertices is bounded above in terms of the aforementioned data.

Keywords

non-negative matricesPerron—Frobenius theoryPerron numbersshifts of finite typeentropy

MSC classification

Primary: 37B10: Symbolic dynamics 37B40: Topological entropy 15A18: Eigenvalues, singular values, and eigenvectors 15B36: Matrices of integers 15B48: Positive matrices and their generalizations; cones of matrices
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 10 , October 2022 , pp. 3246 - 3269
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Banaszczyk, W.. New bounds in some transference theorems in the geometry of numbers. Math. Ann. 296(1) (1993), 625–635.CrossRefGoogle Scholar
Bayer Fluckiger, E.. Upper bounds for Euclidean minima of algebraic number fields. J. Number Theory 121(2) (2006), 305–323.CrossRefGoogle Scholar
Boyle, M. and Handelman, D.. The spectra of nonnegative matrices via symbolic dynamics. Ann. of Math. (2) 133(2) (1991), 249–316.CrossRefGoogle Scholar
Boyle, M. and Lind, D.. Small polynomial matrix presentations of non-negative matrices. Linear Algebra Appl. 355 (2002), 49–70.CrossRefGoogle Scholar
Jarvis, F.. Algebraic Number Theory. Springer, Cham, 2014.Google Scholar
Kim, K., Ormes, N. and Roush, F.. The spectra of nonnegative integer matrices via formal power series. J. Amer. Math. Soc. 13(4) (2000), 773–806.CrossRefGoogle Scholar
Kathuria, L. and Raka, M.. On conjectures of Minkowski and Woods for n = 9. Proc. Indian Acad. Sci. (Math. Sci.) 126(4) (2016), 501–548.CrossRefGoogle Scholar
Lind, D. A.. The entropies of topological Markov shifts and a related class of algebraic integers. Ergod. Th. & Dynam. Sys. 4(2) (1984), 283–300.CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding (Cambridge Mathematical Library), 2nd edn. Cambridge University Press, Cambridge, UK, 2021.CrossRefGoogle Scholar
McMullen, C.. Minkowski’s conjecture, well-rounded lattices and topological dimension. J. Amer. Math. Soc. 18(3) (2005), 711–734.CrossRefGoogle Scholar
McMullen, C.. Slides for dynamics and algebraic integers: perspectives on Thurston’s last theorem, 2014, https://people.math.harvard.edu/~ctm/expositions/home/text/talks/cornell/2014/slides/slides.pdf.Google Scholar
Meyer, Y.. Algebraic Numbers and Harmonic Analysis. (North-Holland Mathematical Library, 2). North-Holland Publishing Co., Amsterdam; American Elsevier Publishing Co., Inc., New York, 1972.Google Scholar
Pisot, C.. La répartition modulo 1 et les nombres algébriques. Ann. Sc. Norm. Super. Pisa Cl. Sci. 7(3–4) (1938), 205–248.Google Scholar
Regev, O., Shapira, U. and Weiss, B.. Counterexamples to a conjecture of Woods. Duke Math. J. 166(13) (2017), 2443–2446.CrossRefGoogle Scholar
Salem, R.. A remarkable class of algebraic integers. Proof of a conjecture of Vijayaraghavan. Duke Math. J. 11(1) (1944), 103–108.CrossRefGoogle Scholar
Schneider, R.. Convex Bodies: The Brunn–Minkowski Theory (Encyclopedia of Mathematics and Its Applications), 2nd edn. Cambridge University Press, Cambridge, UK, 2013.Google Scholar
Siegel, C. L.. Algebraic integers whose conjugates lie in the unit circle. Duke Math. J. 11(3) (1944), 597–602.CrossRefGoogle Scholar
Thurston, W.. Entropy in dimension one. Frontiers in Complex Dynamics: In Celebration of John Milnor’s 80th Birthday, (Princeton Mathematical Series, 51) Eds Bonifant, A., Lyubich, M. and Sutherland, S., Princeton University Press,Princeton, NJ,2014.Google Scholar
Yazdi, M.. Lower bound for the Perron–Frobenius degrees of Perron numbers. Ergod. Th. & Dynam. Sys. 41(4) (2021), 1264–1280.CrossRefGoogle Scholar